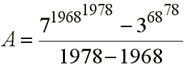|
Rubrique
ENTIER
Question
Le nombre
A = { (7^1968)^1978-(3^68)^78 }
/ (1978-1968)
est-il entier ?
En math, on écrit ce nombre comme ceci (la
formulation ci-dessus permet de communiquer lorsqu'on ne dispose pas de
l'outil formules mathématiques):
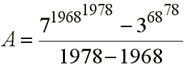
Réponse
La
réponse est OUI
Mais,
voyons tout cela pas à pas
Ne
soyez pas effrayé par la longueur!
J'essaie
de vous donner toutes les étapes pour une bonne compréhension
Outils
Trois
propriétés vont être mises en œuvre
|
§
Un nombre qui se termine par 0 est divisible
par 10
§
Soit deux nombres ayant les mêmes unités: l'unité
de la différence est 0
§
L'unité d'un nombre élevé à une certaine puissance, même très grande, est connu
|
PREMIÈRE ÉTAPE
Divisibilité par 10
|
Voyons ce nombre
|
A =
|
{ (7^1968)^1978 - (3^68)^78 } / (1978-1968)
= N /D
|
|
Le numérateur est un nombre entier
|
N =
|
(7^1968)^1978 - (3^68)^78
C'est une combinaison sans division d'entiers
= entier
|
|
Le dénominateur est facile à calculer
|
D =
|
1978-1968 = 10
|
|
Le problème se résume à démontrer que
|
N =
|
divisible par 10
= 10 k
|
|
En effet
|
A =
|
10k / 10 = k
|
DEUXIÈME ÉTAPE
Différence divisible par 10
|
Comment démontrer que
|
N =
|
10 k
|
|
Décomposons ce numérateur en 2 termes
|
N =
|
C - D
|
|
Avec
|
C =
D =
|
(7^1968)^1978
(3^68)^78
|
|
Quelle est la condition pour que
cette soustraction donne
une différence divisible par 10
|
C & D
|
doivent se terminer par
le même chiffre des unités
|
|
Exemple
|
177 - 57
|
= 120, divisible par 10
|
TROISIÈME ÉTAPE
Unités des puissance de 7
|
Prenons le premier
|
C =
|
(7^1968)^1978
|
|
Unité d'une puissance de 7
On donne la puissance,
puis la valeur de 7 à cette puissance
On remarque que le chiffre des unités
revient selon un cycle de 4 coups
|
|
1, 7
2, 49
3, 343
4, 2401
5, 16807
6, 117649
7, 823543
8, 5764801
9, 40353607
|
|
Règle: Si la puissance divisée par 4
donne un reste de
|
0
1
2
3
|
l'unité est
1
7
9
3
|
|
Dans notre cas, la puissance est
|
p =
|
1968
= 492 x 4
|
|
reste 0
|
|
unité 1
|
|
Il faut encore élever à la puissance
|
q =
|
1978
|
|
un nombre terminé par 1,
élevé à une puissance
se terminera toujours par
|
|
1
|
|
bilan
|
C
|
a 1 pour unité
|
QUATRIÈME ÉTAPE
Unités des puissance de 3
|
Prenons le second
|
D =
|
(3^68)^78
|
|
Unité d'une puissance de 3
On donne la puissance,
puis la valeur de 3 à cette puissance
On remarque que le chiffre des unités
revient selon un cycle de 4 coups
|
|
1, 3
2, 9
3, 27
4, 81
5, 243
6, 729
7, 2187
8, 6561
9, 19683
|
|
Règle: Si la puissance divisée par 4
donne un reste de
|
0
1
2
3
|
l'unité est
1
3
9
7
|
|
Dans notre cas, la puissance est
|
p =
|
68
= 17x 4
|
|
reste 0
|
|
unité 1
|
|
Il faut encore élever à la puissance
|
q =
|
78
|
|
un nombre terminé par 1,
élevé à une puissance
se terminera toujours par
|
|
1
|
|
bilan
|
D
|
a 1 pour unité
|
CINQUIÈME ÉTAPE
Multiple de 10 divisible par 10
|
Le premier terme
|
(7^1968)^1978
|
se termine par 1
|
|
Le second terme
|
(3^68)^78
|
se termine par 1
|
|
leur différence
|
(7^1968)^1978 - (3^68)^78
|
se termine par 0
|
|
Elle est divisible
|
par 10
|
|
|
et
|
par 1978-1968
|
|
|
Et le nombre donné
|
(7^1968)^1978 - (3^68)^78
|
est un multiple de 10
divisé par 10;
c'est un entier
|
|
1978-1968
|
|