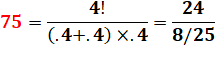Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 05/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	70	71		72	73		74	75	76	77	78	79

Nombre 75	Maths 75	Culture 75	Numération 70 à 79
		Expression 75

Soixante-quinze

Septante-cinq

Seventy-five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	100 1011
Bases	5514 3324
Romain	LXX V

Suite

Caractérisation du nombre

Auto-nombre

Binaire équilibré (autant de "0" que de "1")

Chanceux d'Ulam

Composé

Composé inévitable (ou minimal)

Coster

Cullen moins

Déficient

Impair

Inconsommable

Keith

Narcissique de Keith

Trimorphe

Woodall

Pyramide pentagonale (5^e)

Ennéagonal ou nonagonal (ordre 9) (5^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Ajoutez deux lettres, et Paris devient un paradis:

PAR

AD

IS

Jules Renard

Voir Pensées & humour

CARTE D'IDENTITÉ
Nombre	Composé	Département	PARIS
Facteurs	75 = 3 x 5^2	Élément	RHÉNIUM Re
Propriétés Typiques	Canon de 75 mmm	Mnémo	CALE
	Suite Maths		Suite Culture

Propriétés CULTURELLES

Soixante-quinze

Soixante-quinzième

Septante cinq

Septante cinqième

Voir Orthographe des nombres

Espagnol Italien	Anglais Allemand
setenta y cinco settantacinque	seventy-five fünfundsiebzig

Voir Numération 70 à 79

Nombres et langues

Géométrie	75 polyèdres uniformes	>>>
Géographie	75 Paris	>>>
Quantique	Sur un vaisseau spatial, à 75% de la vitesse de la lumière, un spationaute gagnerait 20 minutes de vie sur ses collègues à Terre.	>>>
Défense	Canon de 75 mm	>>>
Religion	Les Évangiles ont été écrits au plus tard 75 ans après la vie de Jésus	>>>

---

Propriétés MATHÉMATIQUES

Chiffres et numération

7510 = 10 234 = 64 + 0 + 8 + 3	Le plus petit pannumérique en base 4.
75 × (7 + 5) = 900 = 30²	Devient carré en le multipliant par la somme de ses chiffres.
75 = 7+5 + 1+7+7+9+7+8+5+1+5+6+2+5 = 7+5 + 5+6+2+5 + 1+0+0+1+1+2+9+1+5+0+3+9+0+6+2+5 75^2 = 5 625 75^6 = 177 978 515 625 75^8 = 1 001 129 150 390 625		Narcissique de Keith Somme de ses chiffres et de ceux de sa puissance 8; somme de ses chiffres et de ses puissance 2 et 8. Voir Table des nombres de Keith

Addition et soustraction

75 = 3 + 4 + … + 12	Une des cinq sommes de nombres consécutifs >>>
75 = 1 + 5 + 12 + 22 + 35	Somme des cinq premiers nombres pentagonaux. Nombre pyramide pentagonal.
7 + 5 = 12 5 + 12 = 17 12 + 17 = 29 17 + 29 = 46 29 + 46 = 75	Nombre de Keith.
75 = 3 + 5 + 7 + 11 + 13 + 17 + 19	Somme de premiers consécutifs.
xy + x + y ne donne jamais 75	Auto-nombre.
75	Nombre chanceux d'Ulam.
75 => 7 + 5 = 12, 5 + 12 = 17 puis: 29, 46, 75	Keith et Fibodiv: Avec 7 et 5 comme premiers nombres, la somme du type Fibonacci crée une suite où le nombre est présent.

Multiplication, division, diviseurs

75 = ¾ 100 = 3 x 25	Trois quarts de cent.
Facteurs de 75 = {3, 5} + 5 => { 8, 10} qui divisent 75 + 5 = 80 + 9 => {12, 14} qui divisent 75 + 9 = 84			Nombre doublement facteur-diviseur.
23, [75, 1 215, 1 647, 2 624] 75 = 3x5² et 76 = 2²x19 => 38 – 15 = 23			Plus petit nombre tel que son radical est égal au radical du suivant moins k donné.
75 – 2^k avec k de 1 à 6 => 73, 71, 67, 59, 43, 11			Sont tous premiers.
			Nombres Fiancés
			Oméga est la quantité de facteurs distincts. Leur somme pour quatre nombres consécutifs est égale à 9. Le plus petit cas.
10^n – 5^n = 5^n (2^n – 1)		Divisible par 75 pour n pair et par 5 pour n impair.

Avec les puissances

75 = 38² – 37² = 38 + 37	Motif général pour tout nombre impair.
75 = 1² + 5² + 7² = 5² + 5² + 5²		Somme de carrés. Les deux seules pour deux ou trois termes.
75 = 1^3 + 1^3 + 1^3 + 2^3 + 4^3		Somme de cubes.

En puissance

75^2 = 5 625 166^2 = 27 556	Plus petite puissance avec deux "5". Plus petit avec deux "5" d'affilé.
75^3 = 421 875	Nombre plaqué cube ou trimorphique.
75^9 = 75 084686279296875	Nombre qui se retrouve en tête d'une de ses puissances.
2^75 + 75 = 3, 77… 10^22 = 37 778 931 862 957 161 709 643	Motif qui donne un nombre premier.
75 x 2^75 – 1 est premier	Nombre de Woodall (5^e).

Autour du nombre

e^75 – E = 0,0143	Exponentielle proche d'un entier.
75 x 2^75 – 1 = 0, 28 10 ^25 = 2833419889 7217871282 17599 = nombre premier	Nombre de Woodal (5^e).

Jeux et curiosités

75 x 77 = 5 775	Produit qui contient ses opérandes.
	Jeu du quatre 4. Avec .4 = 0, 4 = 2/5

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 0, 1, 0, 1, 1] 3, [2, 2, 1, 0] 4, [1, 0, 2, 3] 5, [3, 0, 0] 6, [2, 0, 3] 7, [1, 3, 5] 8, [1, 1, 3] 9, [8, 3] 10, [7, 5] 11, [6, 9]	12, [6, 3] 13, [5, 10] 14, [5, 5] 15, [5, 0] 16, [4, 11] 17, [4, 7] 18, [4, 3] 19, [3, 18] 20, [3, 15] 21, [3, 12]	22, [3, 9] 23, [3, 6] 24, [3, 3] 25, [3, 0] 26, [2, 23] 27, [2, 21] 28, [2, 19] 29, [2, 17] 30, [2, 15] 60, [1, 15]	14, [5, 5] 24, [3, 3] 74, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 76 Voir en haut de page DicoNombre
Cette page	http://villemin.gerard.free.fr/NombDico/Nb50a100/Nb75.htm