|
||||||||||||
![]()
|
Triplets, primitifs ou non, jusqu'à
500. Toutes les valeurs de u et v pour leur calcul. |
Production
de chaines de triplets sans fin à volonté
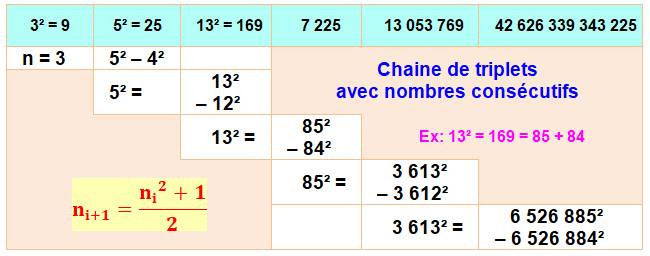
Chaine
possible pour tout nombre impair (ex:
11, 61, 1861, 1731661 …)
![]()
|
|
|||
|
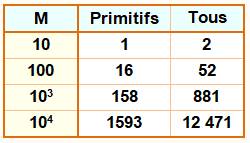
Il existe 16 triplets dont les valeurs (a, b et
c) sont inférieures ou égales à 100. Ils sont 52 en comptant les multiples.
|
Quantité de triplets primitifs jusqu'à 10k 1,
16, 158, 1593, 15919, 159139, 1591579, 15915492, 159154994, 1591549475,
15915494180, 159154943063, 1591549430580, 15915494309496, 159154943089963,
1591549430916326, 15915494309190251, 159154943091887752, 1591549430918979115,
… Quantité de triplets jusqu'à 10k 2,
52, 881, 12471, 161436, 1980642, 23471475, 271360653, 3080075432,
34465432859, 381301109919, 4179478903392, 45459467009968, 491241450001328,
5278882299478796, 56453500988940615, 601181789833245631, … |
||
|
Les 16 triplets primitifs jusqu'à 100 |
[3,
4, 5], [5, 12, 13], [7, 24, 25], [8, 15, 17], [9, 40, 41], [11, 60, 61], [12,
35, 37], [13, 84, 85], [16, 63, 65], [20, 21, 29], [28, 45, 53], [33, 56,
65], [36, 77, 85], [39, 80, 89], [48, 55, 73], [65, 72, 97] |
||
|
Les 52 triplets jusqu'à 100 |
[3, 4, 5], [5, 12, 13], [6, 8,
10], [7, 24, 25], [8, 15, 17], [9, 12,
15], [9, 40, 41], [10, 24, 26], [11, 60, 61], [12, 16, 20], [12, 35, 37], [13, 84, 85], [14, 48, 50], [15,
20, 25], [15, 36, 39], [16, 30, 34], [16, 63, 65],
[18, 24, 30], [18, 80, 82], [20, 21, 29],
[20, 48, 52], [21, 28, 35], [21, 72, 75], [24, 32, 40], [24, 45, 51], [24,
70, 74], [25, 60, 65], [27, 36, 45], [28, 45, 53],
[28, 96, 100], [30, 40, 50], [30, 72, 78], [32, 60, 68], [33, 44, 55], [33, 56, 65], [35, 84, 91], [36, 48, 60], [36, 77, 85], [39, 52, 65], [39, 80, 89], [40, 42, 58], [40, 75, 85], [42,
56, 70], [45, 60, 75], [48, 55, 73], [48,
64, 80], [51, 68, 85], [54, 72, 90], [57, 76, 95], [60, 63, 87], [60, 80,
100], [65, 72, 97] |
||
|
En plus, avec a et b jusqu'à 100 et c libre |
Primitifs: [20, 99, 101],
[60, 91, 109] Tous: [20,
99, 101], [40, 96, 104], [48, 90, 102], [56, 90, 106], [60, 91, 109], [63, 84, 105], [66, 88, 110], [69,
92, 115], [72, 96, 120], [75, 100, 125], [80, 84, 116] |
||
![]()
|
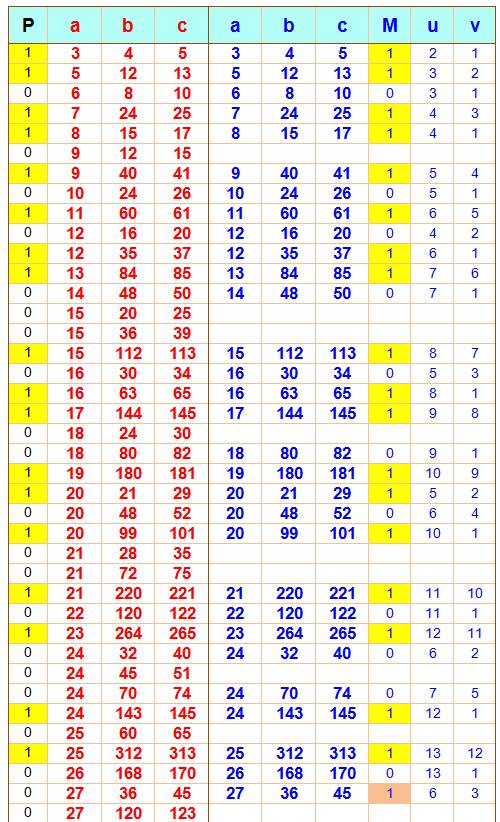
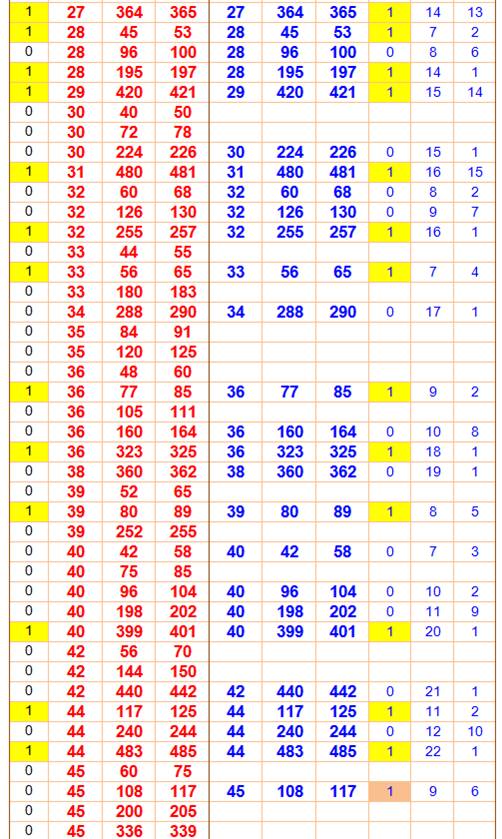
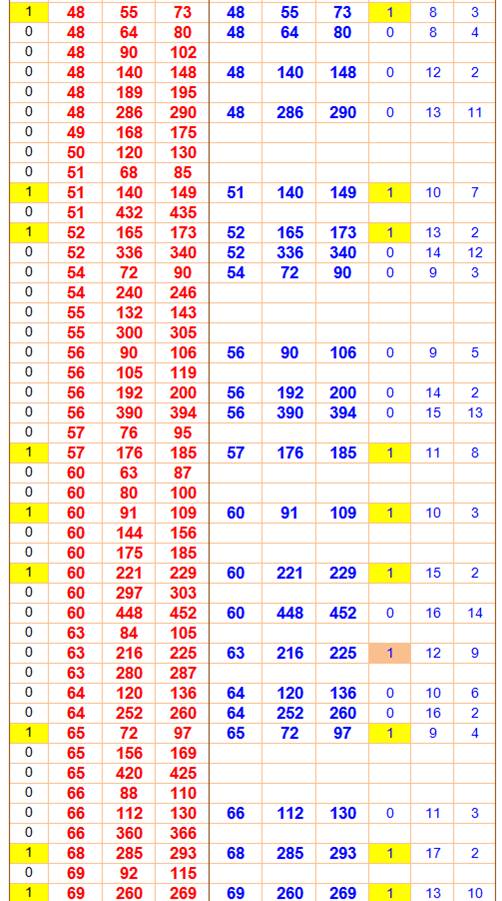
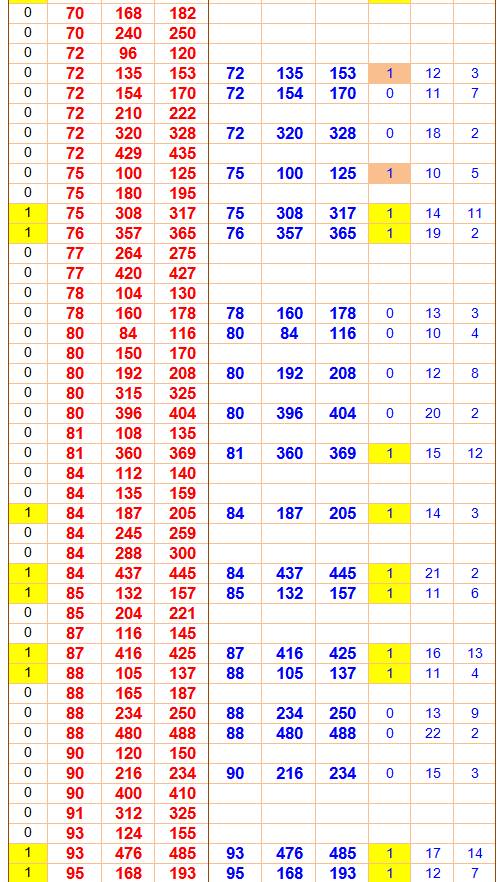
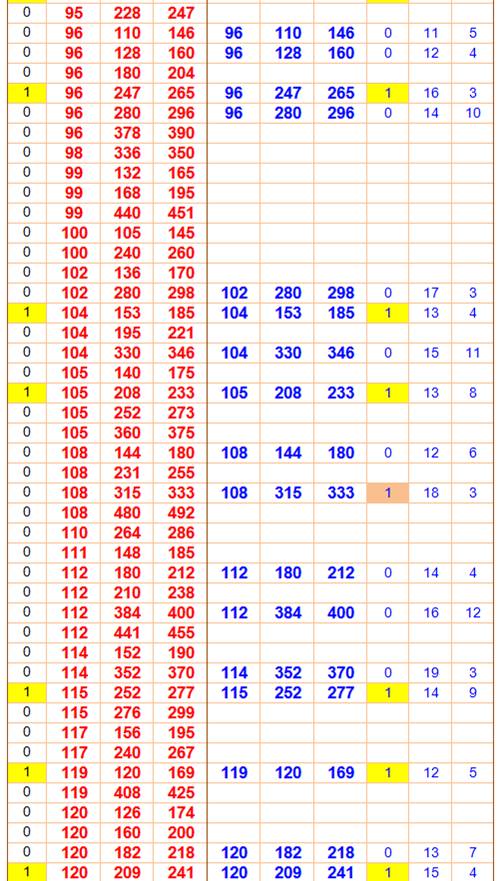
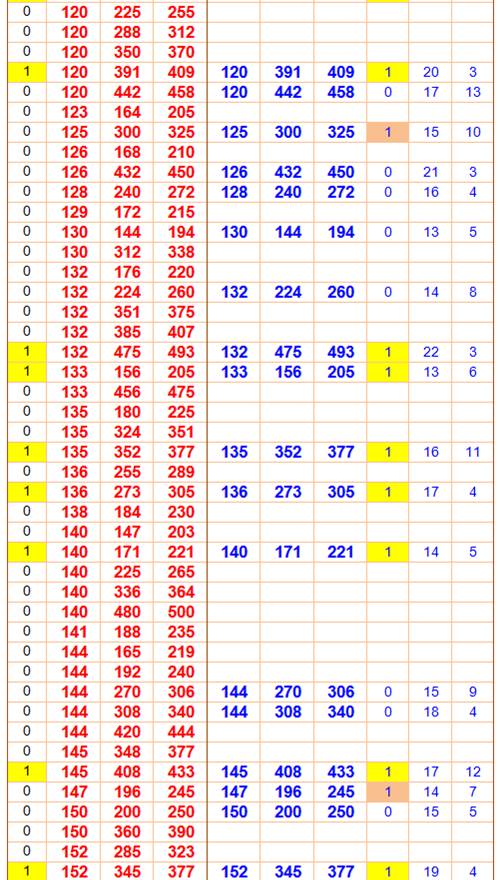
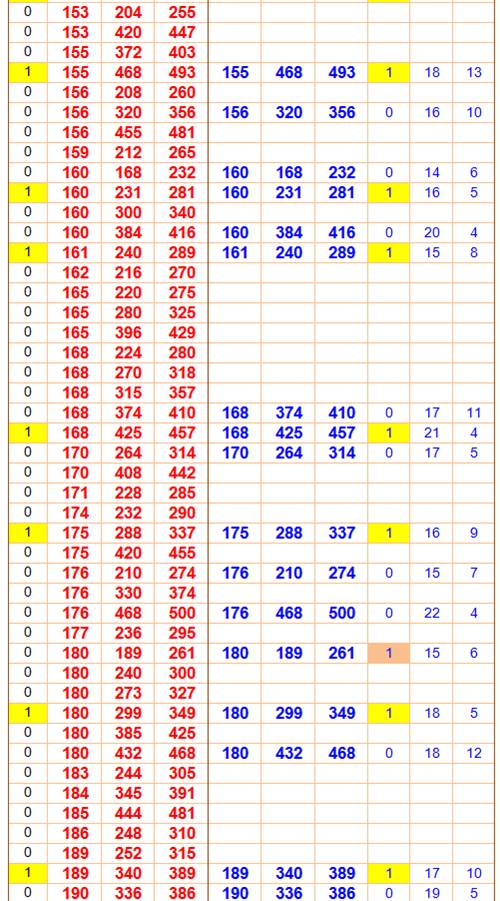
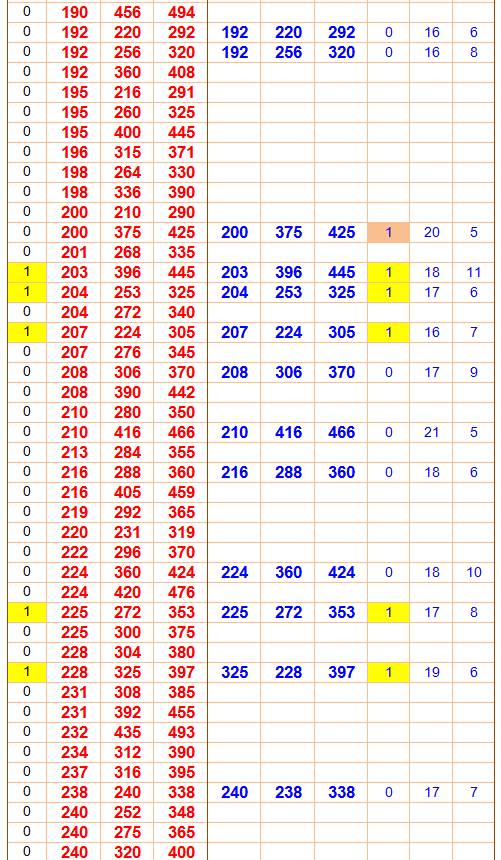
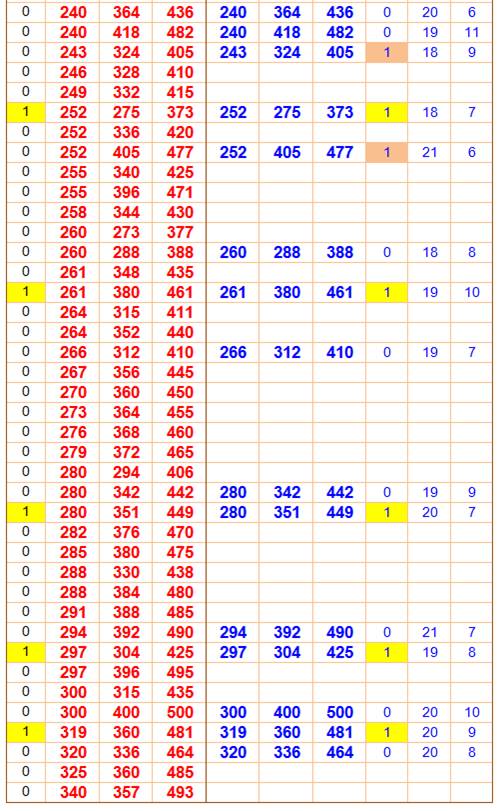
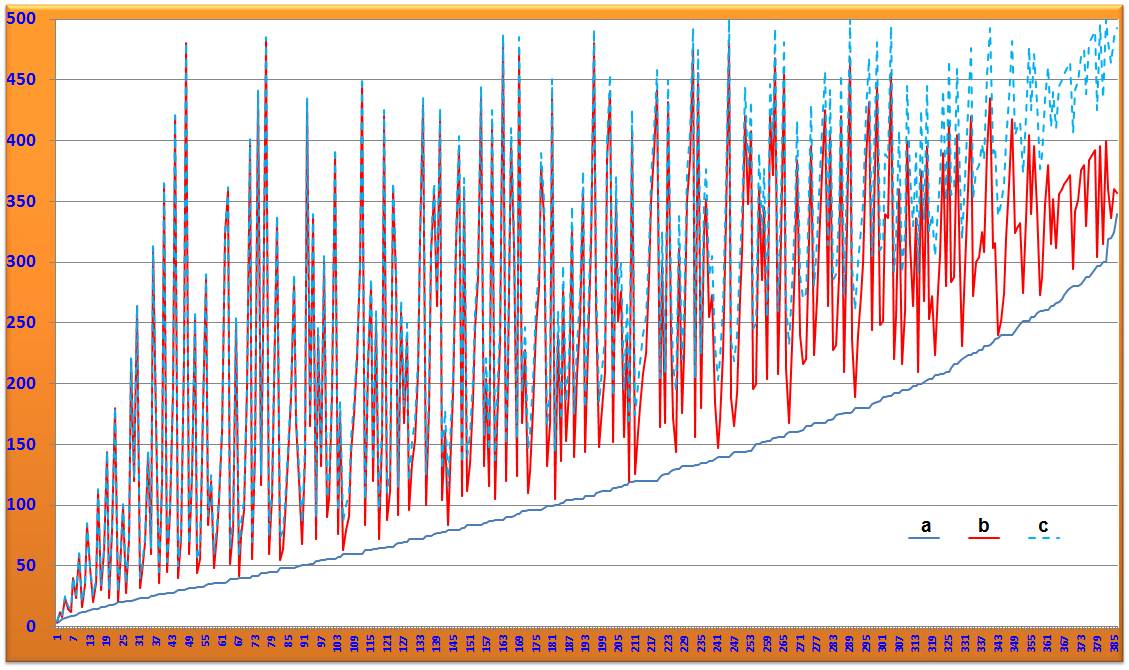
Légende En rouge les 386 triplets
possibles entre 1 et 500 Parmi eux, 80 sont primitifs,
repérés par le 1 en jaune dans la colonne P. En bleu les triplets engendrés
avec les
formules (u² –
v², 2uv, u² + v²)
Les valeurs de u et v sont
indiquées en colonnes de droite. La colonne M indique les cas où u et v sont
de parités opposées. Lecture Le fameux 3² + 4² = 5² est
un triplet primitif (les trois nombres sont premiers entre eux). Il est engendré
par les formules avec u = 2 et v = 1 et les deux composantes additionnées (3
et 4) sont bien de parités opposées (M = 1). Constats 1.
Les
formules en u et v engendrent bien tous les 80 triplets primitifs jusqu'à
500; 2.
Elles
produisent aussi 99 triplets non primitifs, mais pas tous et de loin (ils
sont 306). Ex: (9, 12, 15) qui,
simplifié, n'est autre que (3, 4, 5); 3.
Elles
engendrent aussi des triplets dont les composantes de l'addition sont de
parité opposées sans être premiers entre eux. Ex: (27, 36, 45) qui peut être
réduit en (3, 4, 5). |
Merci à André
Dryvers pour l'aide à améliorer cette page
Tables
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()