|
Édition du: 15/01/2021 |
|
INDEX |
Construction – Cercles tangents |
|||
![]()
|
Constructions de 2 et 3 cercles tangents Construction à
la règle et au compas de cercles
tangents. Pas évident. Méthode sans recourir à l'inversion. |
||
|
|
Sommaire de cette page >>> Deux cercles tangents >>> Trois cercles tangents >>> Rosace de cercles dans hexagone >>> Un cercle tangent à deux cercles quelconques |
Débutants Glossaire |
Résumé
|
Construire un cercle tangent à un autre est simple. Construire un cercle tangent à deux cercles tangents reste assez simple. Construire un cercle tangent à trois cercles tangents devient un défi. La construction
classique fait appel à ce merveilleux outil qu'est l'inversion
géométrique. Sur la page suivante, je présente une solution qui ne nécessite
pas la connaissance de cet outil. Un cercle tangent à quatre
cercles tangents n'existe pas. Les solutions existent aussi bien pour des
cercles internes qu'externes au cercle principal. Le cas d'un cercle tangent à deux cercles quelconques est simple. Le problème d'Apollonius,
construire un cercle tangent à trois cercles quelconques (non tangents) est
plus difficile et n'est pas abordé dans ces pages. La solution passe par
l'emploi de l'inversion. |
|
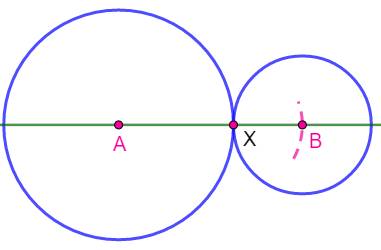
But Construire un cercle de
centre A et de rayon a. Construire un cercle de
centre B et de rayon b, tangent au cercle A. Construction
|
Tracé du second cercle externe au cercle A. Construction semblable pour le cercle B interne
au cercle A. |
|
|
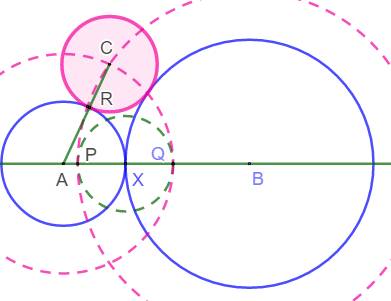
Cercles externes À partir de la figure
précédente, construire un troisième cercle de centre C, tangent aux cercles A
et B. Construction en cinq étapes
|
|
|
|
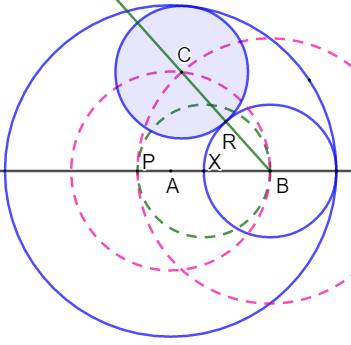
Cercles internes À partir d'un cercle tangent
intérieurement à un cercle, construire le troisième interne tangent aux deux
précédents. Construction
|
Les deux petits cercles sont identiques, mais la
méthode est valable dans tous les cas. |
|
|
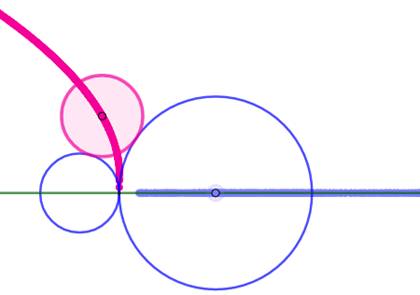
Lieu du point C Lorsqu'on déplace le cercle de droite sur l'axe horizontal,
celui-ci change de taille et le point C se déplace le long d'une hyperbole. Avec les rayons a, b et c des trois cercle, on a: |
|
|
|
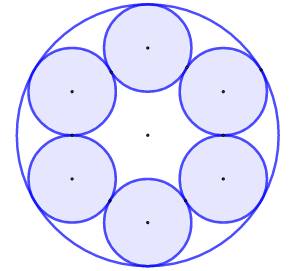
But Créer cette rosace: six cercles tangents inscrits
dans un grand cercle. Principe La construction s'appuie sur
les propriétés de l'hexagone
et de ses diagonales. Défi supplémentaire Insérer six petits cercles
tangents dans les interstices en périphérie. >>> |
|
|
|
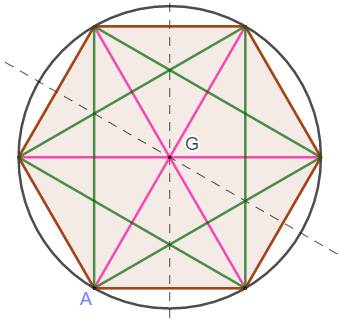
Construction
Observations Les cercles cherchés sont inscrits dans les triangles
équilatéraux en rose. Les centres de ces cercles sont les intersections
des diagonales vertes. |
|
|
|
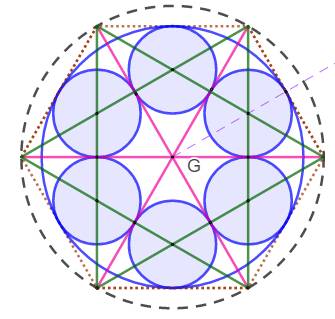
Construction
|
|
|
Voir Rosace complète
avec quatre cercles tangents
|
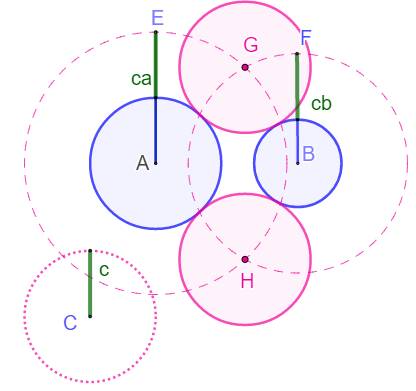
But Construire les cercles G et
H identiques à C, et tangents aux cercles A et B. Construction
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |