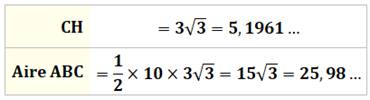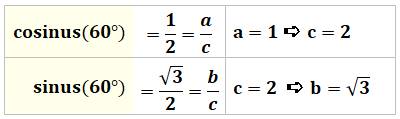Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 18/10/2023 M'écrire Brèves de Maths

INDEX Triangle Géométrie	Triangles – Résolution
	Types de triangles	Résolution	Hauteur	Aire (Héron)
	Construction	Formules	Projection	Triangle 13 14 15
	Hypoténuse	Triangle a 60 b

Faites un double-clic pour un retour en haut de page

Triangle (a, 60°, b) Triangle dont on connait un angle et ses deux côtés adjacents. Calculer l'aire de ce triangle. Trois méthodes.
	Sommaire de cette page >>> Aire du triangle – Calcul classique >>> Aire du triangle – Par le sinus >>> Aire du triangle – Proportions	Débutants Triangle Glossaire Triangle

Aire du triangle – Calcul classique		haut
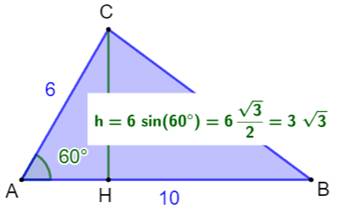
Construction Un triangle dont l'angle A est égal à 60%. La longueur des côtés adjacents est 6 et 10 cm. Calculer l'aire du triangle ABC (dont la valeur indiquée sur la figure est 25,98 cm²). Calcul n° 1 L'aire du triangle est égale à 1/2 fois côté par hauteur. Dessinons judicieusement une hauteur. La hauteur CH est connue par la trigonométrie:

Aire du triangle – Par le sinus		haut
Calcul n° 2 Ce cas avec (longueur, angle, longueur) est connu sous le sigle LAL, un des cas typiques de la résolution des triangles. La formule des sinus pour calculer l'aire s'applique Note Ce calcul est absolument identique au précédent, à ceci, près qu'on se sert de la formule de calcul sans passer explicitement par la hauteur.

Aire du triangle – Proportions		haut
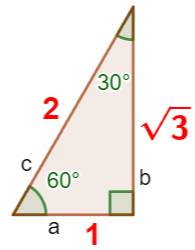
Calcul n° 3 Tous les triangles rectangles avec un angle de 60° sont semblables (les trois angles sont égaux deux à deux). Ils ont tous les mêmes proportions. Prenons un représentant typique dont l'un des côtés de l'angle droit vaut l'unité: le triangle primitif. Les autres côtés s'en déduisent par trigonométrie. Ce triangle primitif, "multiplié" par 3 donne le triangle de notre figure; alors, h = 3√3 et l'aire A = 15 √3.	Triangle primitif de tous les triangles rectangles avec angle de 60°

Haut de page (ou double-clic)

Retour	T 13 14 15
Suite	Formules pour résoudre les triangles Résolution des triangles LLL Constructions élémentaires: les triangles
Voir	Triangle entier (17, 24, 25, 26) Triangles héroniens Triangle – Introduction Triangle – Index Volume du tétraèdre Formule de Héron pour le trapèze
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/Trga60b.htm