|
Édition du: 28/03/2023 |
|
INDEX |
GRAPHES |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
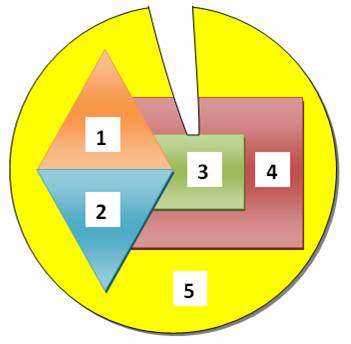
CINQ PAYS Comment
représenter cinq pays sur une carte, chacun ayant des frontières communes
avec les quatre autres? |
||
|
|
Sommaire de cette page >>> Problème des cinq pays |
Débutants Glossaire |
|
|
||
|
|
Le théorème des quatre
couleurs est démontré (certes difficilement et avec ordinateur). Il est toujours possible
de colorier une carte avec quatre couleurs seulement. Si un cinquième pays avait des frontières communes avec les quatre
autres, il faudrait une cinquième couleur pour le colorier. Ce qui est
contraire au théorème. |
|
|
|
|
|
|
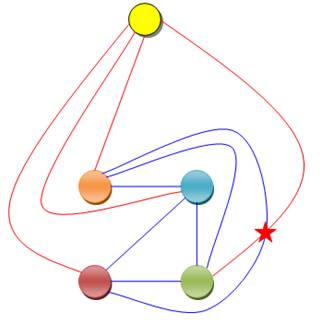
Le graphe K5, comme le K3,3 ne sont pas
coplanaires.
|
|
|
![]()
![]()