|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite de nombres dite du COMMENTAIRE NUMÉRIQUE Suite de Conway Suite de nombres comportant une autoréférence. Elle mixte nombres et quantité de nombres. |
|
Anglais: Likeness
sequence / Look-and-say sequence
/ Audioactive decay (terme de Conway,
auteur de cette suite en 1986) Allemand: Gleichniszahlen-Reihe
(terme de Hilgemeier) |
|
|
|
|
Une suite
mystérieuse 1 11 21 1211 111 221 ?..
La clé du mystère
Autre écriture pour
comprendre le truc 1, 11, 21, 1211, 111221, 312211 … 1, un
1, deux 1, un
2 un 1,
trois 1 deux
2 un 1 … La suite 1 11 21 1211 111221 312211 13112221 1113213211 31131211131221 13211311123113112211 11131221133112132113212221 3113112221232112111312211312113211 …
|
|
|
|
||||||||||||||||
|
||||||||||||||||
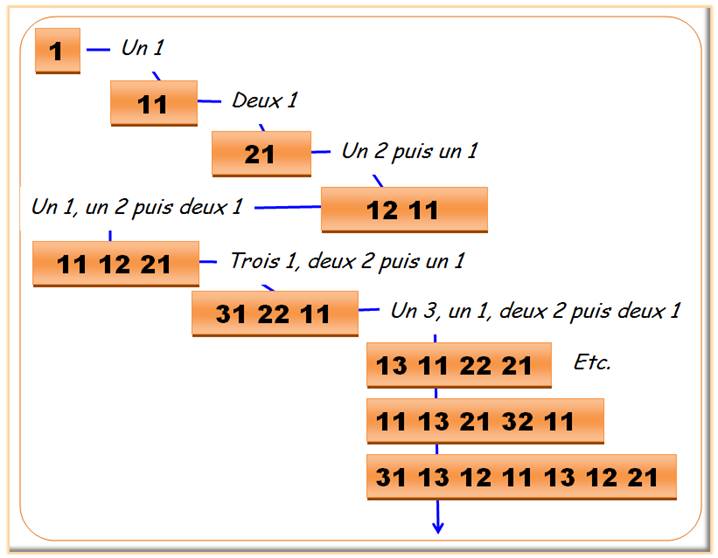
Explications illustrée
|
|
||
|
|
Il
y a un " 1 ", on écrit: 11 sur la ligne suivante. |
|
|
|
Il
y a deux " 1 ", on écrit: 21 |
|
|
|
Il
y a un " 2 " puis un " 1 ", soit 12
11. |
|
|
|
Etc. |
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Il
y a 1 U |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Il
y a 1 U, 1 N et 1 U |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Etc. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Illustration
Autre forme
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Générales
La preuve:
supposons que 333 soit en position n pour la première fois, ce 333 voudrait
dire qu'il y a aussi trois 3 avant, ce qui est contradictoire.
|
|
|
|
||
|
Les
éléments stables
Exemple:
N = GD (partie gauche et partie droite) |
||
|
G =11132 |
D = 13211 |
|
|
Tous les commentaires
suivant se termineront par 2. |
Aucun des
commentaires suivants ne commencera par 2. |
|
|
311312 1321131112 11131221133112 |
11131221 3113112211 13211 3212221 |
|
|
La fin est toujours
2. |
Le début revient de
manière cyclique. |
|
|
|
||
|
|
||||||||||||||||||||||
|
Commentaires
cycliques
Commentaire
de suite finies
Ces suites ne sont
pas infinies, elles donnent un cycle. Exemple en partant de
1
|
||||||||||||||||||||||
|
|
|
|
|
|
![]()
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()
