|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Quels
sont les relations de divisibilité entre
un nombre donné et ses chiffres ? |
|
|
Il est divisible
par chacun de ses chiffres (nombre
nu) |
224 =
2 × 112 = 4 × 56 |
|
Idem avec chiffres tous différents (Lynch-Bell) |
248 =
2 × 124 = 4 × 62 = 8 × 31 |
|
Idem mais avec un reste de 1 (Chiffres mod 1) |
289 =
2 × 144 + 1 = 8 × 36 + 1 = 9 × 32 +
1 |
|
Il est divisible
par les chiffres des extrémités (fourchette) |
104275
= 1075 × 97 |
|
Il est divisible
par la somme de ses chiffres (Harshad) |
198 = (1+9+8)
× 11 = 18 × 11 |
|
Il est divisible
par le produit de ses chiffres (Zuckerman) |
384 = (3×8×4) × 4 =
96 × 4 |
|
Il est divisible
par la somme et produit du carré ses
chiffres (nombre
insolite) |
122
121 216 = 56 × 2 180 736 = 9 216 × 13 251 |
Voir Brève 62-1231 / Chiffres –
Index
|
|
||
|
Approche |
|
|
|
Définition |
Nombre sans zéro divisible par
chacun de ses chiffres. A number is
nude if it is divisible by all of its digits (which should be nonzero). The
number is called "nude" because it exposes some of its factors. |
|
|
Exemple |
784 = 7 x 112 = 8 x 98 = 4 x 196 |
|
|
Liste |
1, 2, 3, 4, 5, 6, 7,
8, 9, 11, 12, 15, 22, 24, 33, 36, 44, 48, 55, 66, 77, 88, 99, 111, 112, 115,
122, 124, 126, 128, 132, 135, 144, 155, 162, 168, 175, 184, 212, 216, 222,
224, 244, 248, 264, 288, 312, 315, 324, 333, 336, 366, 384, 396, 412, 424,
432, 444, 448, 488, 515, 555, 612, 624, 636, 648, 666, 672, 728, 735, 777,
784, 816, 824, 848, 864, 888, 936, 999, 1111, 1112, 1113, 1115, 1116, 1122,
1124, 1128, 1131, 1144, 1155, 1164, 1176, 1184, 1197, 1212, 1222, … OEIS
A034838 - Numbers k that are divisible by every digit of k |
|
|
Propriétés |
C'est Y. Katagiri qui a baptisé ces
nombres (1982-83). Tous les repdigits sont des nombres nus (trivial).
Donc, les nombre snus sont en nombre infinis. L'ensemble des nombres nus est un
sous-ensemble des nombres sans "0". Si un nombre nu contient un 5, alors
les autres chiffres sont impairs. (un
nombre divisible par 5 ne peut pas être pair). Le nombre 735 est sans doute le seul
nombre nu sans "1" dont les chiffres sont premiers deux à deux. Le plus petit nombre nu qui contient
tous les chiffres impairs est 1117935. |
|
Merci à Christian Amet pour ses remarques
|
|
||
|
Définition |
Nombre à chiffres
distincts sans zéro divisible par chacun de ses chiffres. Lynch-Bell
numbers: numbers n such that the digits are all different (and do not include
0) and n is divisible by each of its individual digits. |
|
|
Exemple |
784 = |
|
|
Liste |
1, 2, 3,
4, 5, 6, 7, 8, 9, 12, 15, 24, 36, 48, 124, 126, 128, 132, 135, 162, 168, 175,
184, 216, 248, 264, 312, 315, 324, 384, 396, 412, 432, 612, 624, 648, 672, 728,
735, 784, 816, 824, 864, 936, 1236, 1248, 1296, 1326, 1362, 1368, 1395, 1632,
1692, 1764, 1824,… |
|
|
|
||
|
Approche |
|
|
|
Définition |
Nombre qui est divisible par le
produit de ses chiffres. Les nombres
contenant un 0 sont naturellement exclus. Alors que les nombres de Harshad sont divisibles par la somme. |
|
|
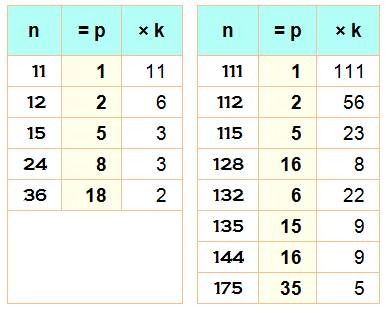
Exemples |
|
|
|
Liste |
1, 2, 3, 4, 5, 6,
7, 8, 9, 11, 12, 15, 24, 36, 111, 112, 115, 128, 132, 135, 144,
175,
212, 216, 224, 312, 315, 384, 432, 612, 624, 672, 735, 816, 1111, 1112, 1113,
1115, 1116, 1131, 1176, 1184, 1197, 1212, 1296, 1311, 1332, 1344, 1416, 1575,
1715, 2112, 2144, 2232, 2916, 3111, … |
|
|
Propriétés |
Un nombre de Zuckerman est un nombre
nu. Un nombre de Zuckerman ne contient
jamais un 2 et un 5 à la fois, car le nombre se terminerait par 0 et, ce
zéro, annulerait le produit. Le plus petit Zuckerman contenant
les huit chiffres possibles est: 1 196 342 784 |
|
Voir Compléments
en Brève de Maths n°231
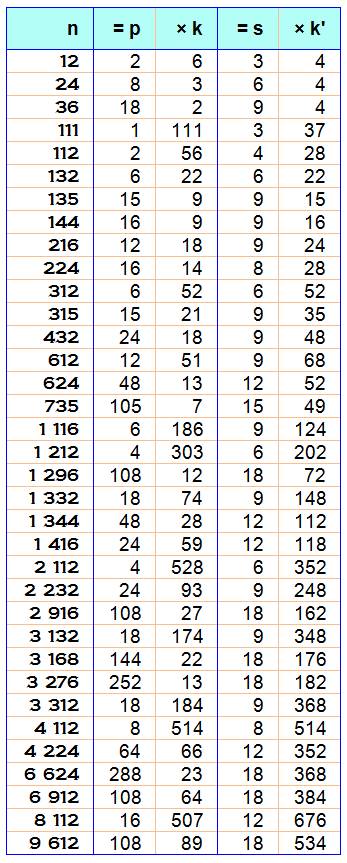
Nombres à la fois Zuckerman et
Harshad
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Zuckerma.htm
|
![]()