NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/03/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Division	Divisibilité		Glossaire Division
INDEX Somme des chiffres Formes et motifs Nombres en chiffres Chiffres Décomposition Itérations	Index divisibilité	Racine Numérique	Critères
		Clé de divisibilité	Curiosités
		Sommaire de cette page >>> Approche & curiosité >>> Somme numérique >>> Preuve par 9 >>> Principe de la preuve par 9 >>> Vision modulo >>> Signature numérique

RACINE NUMÉRIQUE d'un nombre

PREUVE par neuf

ou RÉSIDU

Le calcul de la somme (ou racine) numérique d'un nombre permet une vérification rapide des opérations. La preuve par neuf en est une application bien connue.

Autre nom: persistance additive des nombres

Exemple:

Voir Débutants / Preuve par neuf – Glossaire / Divisibilité par 9 / Racine multiplicative
Anglais: Digital root or repeated digital sum

APPROCHE & CURIOSITÉ
Prenons un nombre:	123
Ce nombre n'est pas divisible par 9 ?	123 = 13 x 9 + 6
Le reste de la division par 9 est:	6
Décomposons ce nombre:	123 = 100 + 20 + 3
Observons le reste de chaque terme en le divisant par 9 :	100 = 11 x 9 + 1 20 = 2 x 9 + 2 3 = 0 x 9 + 3
N'est-ce pas troublant: on retrouve le nombre du départ.	1, 2 & 3
Encore plus bluffant: la somme des chiffres est égale au reste de la division.	1 + 2 + 3 = 6
Encore une observation intéressante: la soustraction du nombre et du reste.	123 – 6 = 117
Or cette différence est aussi divisible par 9.	117 = 13 x 9
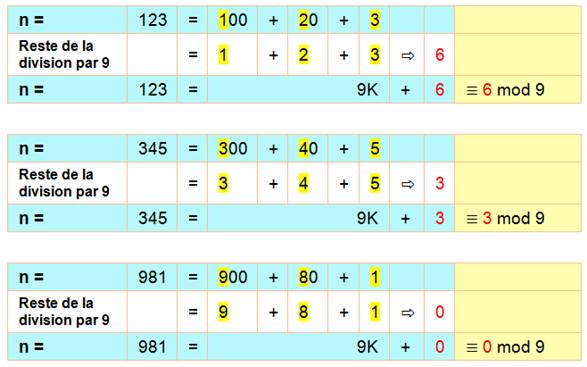
Retenons pour le moment, et sous réserve de preuves Le reste de la division par 9 d'un nombre n = abc, est la somme de ces chiffres r = a + b + c. La différence n – r est divisible par 9.

Somme Numérique, ou Racine Numérique ou Résidu
La somme numérique est la somme des chiffres d'un nombre; la somme est éventuellement répétée jusqu'à obtenir un seul chiffre. Note: la somme numérique d'un nombre formé de 9, est égale à 9. Ajouter un 9 ne change pas la somme numérique.	n = 456 SN = 4 + 5 + 6 = 15 SN = 1 + 5 = 6 n = 999 SN = 9 + 9 + 9 = 27 SN = 2 + 7 = 9
Le 9 est neutre dans la somme numérique. On l'élimine autant que possible. Note: calcul rapide de la somme numérique en groupant les somme donnant 9, considéré comme 0 en l'occurrence.	n = 456 SN = 9 + 6 SN = 6 n = 123456789 SN = 1+8 + 2+7 +3+6 + 4+5 + 9 SN = 0

Preuve par neuf

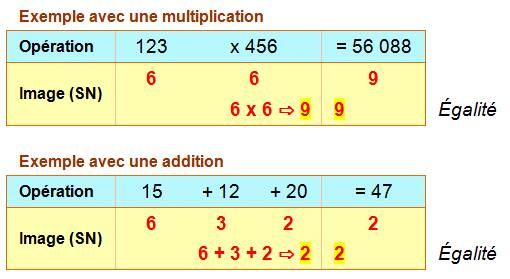
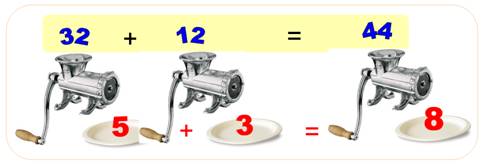
Soit une opération arithmétique. Son image avec les sommes numériques est également correcte. C'est la preuve par neuf. Si une opération est juste, la même opération sur les sommes numériques est également juste. Nous venons d'effectuer une preuve par neuf. Applications aux opérations >>> Notez bien que, si l'égalité des racines numériques est vraie, l'opération peut être fausse; il suffit que plusieurs erreurs se compensent pour donner les sommes numériques qui conviennent. Néanmoins, si l'égalité est fausse, il est certain que l'opération est fausse. Il existe aussi une preuve par 11, un peu moins pratique, il est vrai.

PRINCIPE de la PREUVE PAR 9

Observations Notons tout de suite que 9 ne divise aucun des nombres: 10, 100, 1000 … 10^n. Voyons les restes de la division par 9 de ces nombres et leurs multiples: Conclusion Reste de (a x 10^k / 9) = a On dit: dans le monde de la division par 9, ce nombre a un reste égal à a. Ou encore: en coupant le nombre en tranches (en modules) de 9, il reste un morceau égal à a. En abrégé: ce nombre modulo 9 a. (signe égal à trois barres pour montrer une "égalité" dans le monde des modulos) Applications

Voir Calculs pratiques

VISION MODULO – Théorie

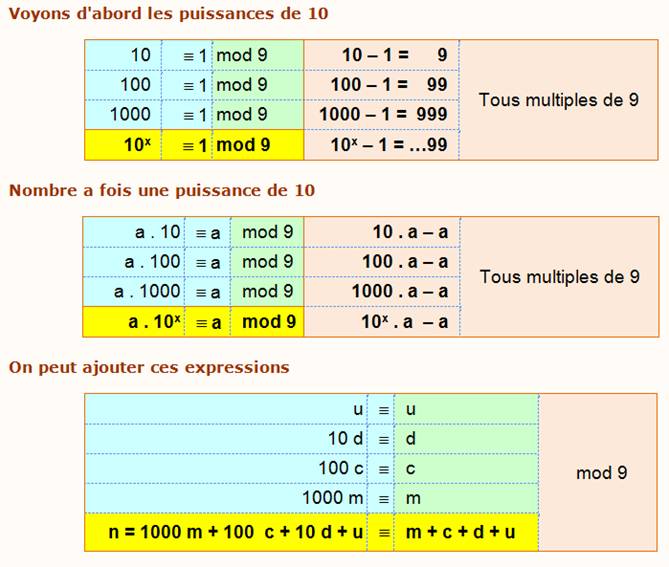
Exploitons la vision modulo pour formaliser les résultats que nous venons d'observer. Le modulo 9 d'un nombre est la somme de ses chiffres, soit sa somme numérique. Conséquence Tout nombre n = … + 1000 . m + 100 . c + 10 . d + a diminué de la somme de ses chiffres r = ... m + c + d + u est divisible par 9. Cas de l'élimination des 9 Lors du calcul de r, on peut éliminer les 9 dès qu'ils apparaissent. En effet: On cherche une différence divisible par 9. On peut y retirer autant de 9 que l'on veut, sans changer le caractère de divisibilité. Si (n – a) est divisible par 9 alors (n – a – 9) est encore divisible par 9. D'ailleurs, en anglais, la preuve par 9 est appelée Casting out nines (éliminer les neufs).

Signature numérique
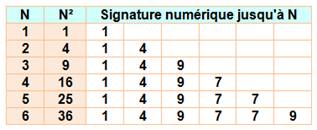
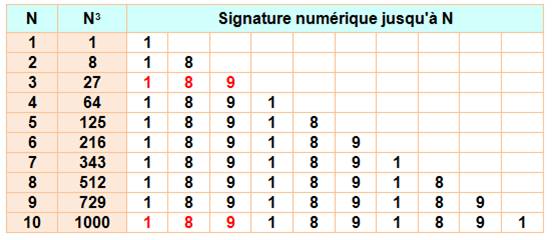
Signature numérique des carrés N et son carré; on calcule la racine numérique du carré. La suite de ces RN est: 1, 4, 9, 7, 7, 9, 4, 1, 9, 1, 4, 9, 7, 7, 9, 4, 1, 9, 1, 4 … Le nombre récurrent est la signature numérique.	1 497 799 419
Signature numérique des cubes = 189
Nombres triangulaires	136 163 199
Nombres triangulaires centrés	141
Nombres carrés centrés	154 757 451
Auto-nombres	135 792 468
Nombres Demlo	149 779 419
Nombres pentagonaux	153 486 729
Nombres hexagonaux	166 193 139

Suite	Critères de divisibilité par 2, 3, … Divisibilité – Index Somme des chiffres de diverses natures Spectre numérique Nombres de Harshad Somme et produit des chiffres – Index Persistance multiplicative
Voir	Calcul mental – Index Clé de divisibilité Divisibilité des triplets de Pythagore Divisibilité pour juniors Factorisation d'un nombre Géométrie – Index Nombres parfaits  Preuve - Glossaire Racine carrée, cubique … Radical d'un nombre Somme des carrés des chiffres Théorie des nombres – Index
DicoNombre	Nombre 189 Nombre 3 367 Nombre 381 654 729
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/RaciNume.htm