NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Général	ENTIERS			Glossaire Général
INDEX Type de nombres	Nombres entiers		Entier en polynôme
		Sommaire de cette page >>> Formes polynomiales donnant un entier >>> Démonstration par induction >>> Autres formes polynomiales donnant un entier

Voir Nombres entiers

Formes polynomiales donnant un entier
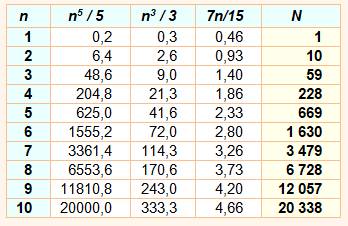
Affirmation Montrez que l'expression suivante est un nombre entier: N = n^5/5 + n^3/3 + 7n/15 Réduction au même dénominateur	Exemples

Voir Divisibilité des polynômes

Démonstration par induction

Pour k = 1, c'est vrai

n^5	+	n^3	+	7n	=	1	+	1	+	7	= 1
5		3		15		5		3		15

Supposons la formule vraie pour k,

L'est-elle pour k + 1?

m =	k^5	+	k^3	+	7k
	5		3		15

m' =	(k+1)^5	+	(k+1)^3	+	7(k+1)
	5		3		15

15 m' = 3(k+1)⁵ + 5(k+1)³ + 7(k+1)

Rappel du développement du binôme en utilisant le triangle de Pascal

2	=>				1		2		1
3	=>			1		3		3		1
4	=>		1		4		6		4		1
5	=>	1		5		10		10		5		1

Développons 15m'

15m' =

3 k^5	+ 3 x 5k^4	+ 3 x 10k^3	+3 x 10k^2	+ 3 x 5k	+ 3 x 1
		+ 5 x k^3	+ 5 x 3k^2	+ 5 x 3k	+ 5 x 1
				+ 7k	+7
= 3 k^5	+ 15k^4	+ 35k^3	+45k^2	+ 37k	+ 15

En divisant par 15 et en ordonnant pour mettre en évidence m.

En fait m est la somme de m qui est supposé être un entier, et d'un polynôme en k qui lui aussi donne un entier.

Alors la somme de ces deux termes entiers est un entier

CQFD.

m' =	k^5	+ k^4	30k^3	+	5k^3	+ 3k^2 +	30k	+	7k	+ 1
	5		15		15		15		15

m' =	k^5	+	k^3	+	7k	+ k^4 + 2k^3 + 3k^2 + 2k + 1
	5		3		15

m' = m + k⁴ + 2k³ + 3k² + 2k + 1

Autres formes polynomiales donnant un entier

On montrerait de la même manière que les expressions suivantes donnent des nombres entiers:

n^7	+	n^5	+	n^3	+	n^2	–	37n
7		5		3		2		210

n^11	+	n^5	+	n^3	+	62n
11		5		3		165

Suite	Démonstration par récurrence
Voir	Algèbre – Les bases Type de nombres Inverses et formes polynomiales
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/Entier.htm