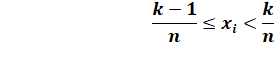|
Édition du: 01/03/2022 |
|
INDEX |
JEUX ARITHMÉTIQUES |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Problème des 18 points Irrégularité de distributions Numéro des villas bien rangées Problème
numérique surprenant. Sur la longueur de la rue, on trouve deux villas dans chacun
des demi-longueurs, trois dans chacun des tiers de longueurs, quatre dans …. On
s'attend à ce que cela soit possible sans fin. Eh bien non! Ce n'est possible
qua jusqu'à un partage en 17 tronçons, soit 18 points. |
||
|
|
Sommaire de cette page >>> Approche avec 4 tronçons >>> Cas de 5 tronçons >>> Le problème original >>> Historique >>> Une solution pour 17 tronçons |
Débutants Glossaire |
|
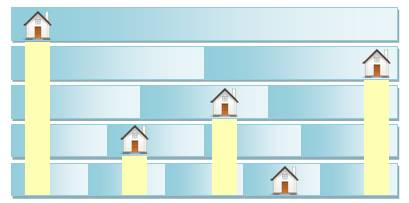
Dans cette rue une première villa s'installe. |
|
|
|
Une deuxième villa est construite dans l'autre
moitié de la rue. |
|
|
|
Le troisième propriétaire a obligation de placer sa
villa dans un des trois tiers non occupé. |
|
|
|
La même obligation est faite au quatrième
propriétaire pour se positionner dans le quart inoccupé. |
|
|
|
Avec une villa de plus, il est encore facile la
placer dans un tronçon d'un cinquième non occupé. Pour vérifier que les conditions sont bien
remplies, on peut partir du bas et compter 5 villas dans la découpe en cinquièmes;
4 villas dans la découpe en quarts; 3 villas dans la découpe en tiers; 2
villas dans la découpe en demis. |
|
|
|
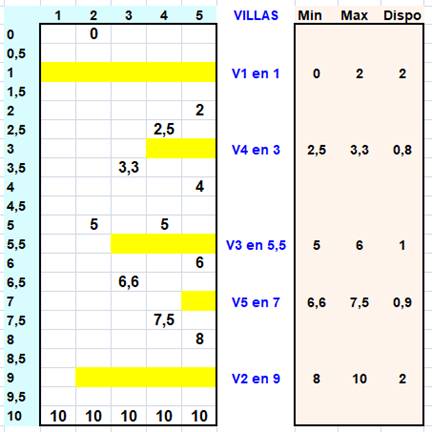
Espace disponible pour chaque villa Sur ce tableau les tronçons sont numérotés en
haut (1, 2, 3, 4, 5). La distance est donnée de 0 à 10 unités en
colonne. Les limites de tronçons sont mentionnées dans le
tableau dans la colonne correspondant au tronçon. Les villas sont positionnées dans les emplacements
libres montrés en jaune. D'autres dispositions sont possibles. Pour cette disposition, on calcule la limite
minimale et la limite maximale pour l'emplacement de la villa (zone ocre). La
disponibilité s'étend de 0,8 à 2 unités de longueur. La villa n°4 ne pourra pas avoir une façade de
plus de 0,8 unité de longueur. |
|
|
Voir Brève
853
|
Trouver N nombres (x1, x2, …,
xN) compris entre 0 et 1 tels que:
Formalisation algébrique
Exemple: Recherche sur 5
rangs (N = 5), au niveau des quarts (n = 4), la villa du rang 2 depuis le
début de la rue (k = 2) se trouve au 0,3 (3 divisé par 10) ce qui satisfait
bien: 1/4 < 0,3 < 2/4. |
|
Ce problème a été publié dans One hundred problems in elementary mathematics par le mathématicien
polonais Hugo Steinhaus. Sa traduction en anglais date de 1964. Son ouvrage cite une solution avec 14 points, et
indique en note de bas de page que M. Warmus a prouvé que 17 est la limite. La première preuve publiée en 1970 est due à
Elwyn R. Berlekamp et Ronald L. Graham dans Irregularities in the distributions of finite sequences. Warmus, mathématicien polonais, publie une preuve
plus courte en 1976. Il fournit une solution en 17 points et indique qu'il en
existe 768 ou le double en comptant les symétriques. |
|
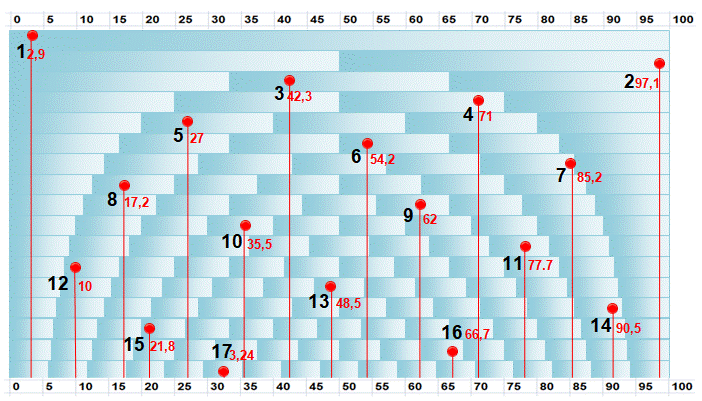
On vérifie qu'en bas de dessin, il existe bien
une "villa" dans chacun des 17 tronçons et qu'il en existe
également une dans chacun des tronçons en seizième, etc.
Il n'est pas très difficile de montrer que 18
n'est pas possible. La majorité des essais au hasard, vous conduira à
un échec bien avant d'atteindre les 17. La vidéo citée en référence
montre comment, en choisissant la villa de neuvième rang en 0,46, un choix
judicieux, les possibilités sont limitées et conduisent inéluctablement à une
impasse. L'auteur trace les segments de possibilités qui sont de plus en plus
petits et tournent à l'impossible. La vidéo est en anglais mais pas trop
difficile à suivre et, bonus, elle est sous-titrée. |
|
Illustration en demi-cercles de la solution en 17 points
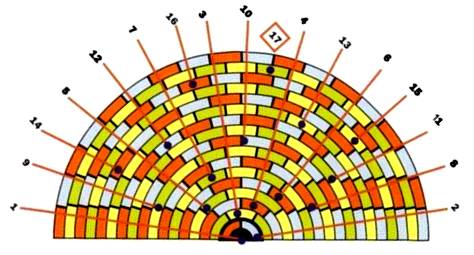
Source Image
par Ivan Moscovich – The eighteenth amendment – Pages 92-93
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Livres |
|
|
Cette page |