|
Édition du: 27/12/2022 |
|
INDEX |
Types de Nombres – Motifs |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
POINTS PROCHES Un nombre donné
de points distincts sont répartis au hasard sur une figure. Combien en faut-il
pour qu'ils soient tous à une distance maximale les uns des autres ? |
||
|
|
Sommaire de cette page >>> Sur un segment >>> Sur un cercle |
Débutants Glossaire |
|
Question Sur
un cercle de 10 cm de circonférence, on place des points au hasard. Combien
en faut-il pour que chacun soit à moins de 1 cm d'un autre ? |
Solution Examinons
des cas plus simples pour se familiariser: le segment. |
|
|
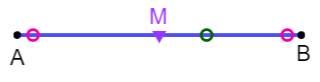
Trois points distincts sur un segment de 1 cm Distance
maximale entre deux points: 0,5 cm En
effet, dans le cas extrême où deux points sont sur les extrémités du segment,
le troisième point est quelque part dans une des deux moitiés (AM ou MB),
soit à moins de 0,5cm de l'un d'eux. |
|
|
|
Quatre points distincts sur un segment de 4 cm Supposons
trois points proches des extrémités A et C distantes de 2 cm. Dans
le cas extrême où le quatrième point
se situe sur le point B, alors ce point est toujours à une distance
inférieure ou égale à 1 cm de l'un des trois autres. |
|
|
|
k points distincts sur un segment k cm Aucun
point n'est à une distance supérieure à 1 cm d'un autre. |
|
|
|
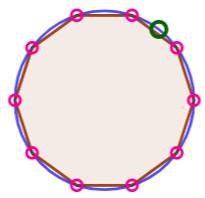
Onze points sur un cercle Quelle
est la taille du cercle pour que dix points distincts répartis sur la
circonférence soient au plus éloigné de 1 cm ? Selon
ce qui a été vu ci-dessus, il faut dix arcs de cercle mesurant 1 cm, soit une
circonférence de 10 cm. Si
dans le cas le plus extrême, les dix points sont sur les sommets du décagone
inscrit, le onzième sera entre deux points et à moins d'un centimètre de l'un
d'eux. Il existe deux points qui partagent le même arc de 1 cm. |
|
|
|
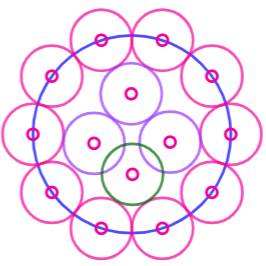
Treize points dans le disque Cercle
formé de dix arcs de 1 cm (R = 1,59 cm). Dés
que l'on place treize points distincts au hasard dans ce disque, ils sont
tous à moins de 1 cm d'un autre. Le
cercle représente une distance à moins de 1 cm du point. Dans
le cas extrême où dix points sont sur la circonférence, chacun éloigné de 1
cm des autres (cercles roses), il est possible de loger trois autres points éloignées
1 cm ou plus de l'un des autres (cercles violets). Mais le treizième est
toujours à moins de 1 cm d'un autre (cercle vert). La
démonstration n'est pas simple >>> |
|
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |