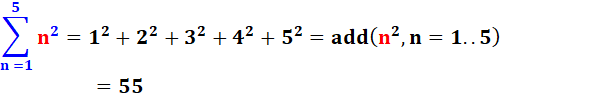|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Sommes particulières avec les nombres Approche – Introduction
– Pistes Application du calcul de la
somme à des nombres particuliers notamment, la suite des nombres qui
commence par 1 ou la suite de ces mêmes nombres mis au carré,
etc. |
Notations des sommes
|
Le symbole
"grand sigma" résume
une somme qui est souvent longue si développée
complètement. Lecture: la somme de
n au carré pour les valeurs de n allant de 1 à 5 est égale à
1² + 2² + 3² + 4² + 5². On peut la noter de
façon linéaire et
sans ce symbole avec add (souvent utilisée par les langages de programmation). |
![]()
|
|
|
|
On distingue plusieurs
grandes catégories de sommes de nombres dont voici les grandes
catégories. On retrouvera le
détail de toutes ces sommes dans l'index >>> |
|
|
Type 1: on se propose
de calculer la somme de nombres portés ou non à une puissance.
Objet de ces
pages sur les sommes de nombres Une telle somme est
formée d'uns suite de nombres et la
somme est nommée série. La
suite peut être finie (de 1 à
n) ou infinie. Voir Suites et
Séries / Infini |
|
|
{1, 2, 3,…}k |
Somme des nombres successifs,
chacun porté à la même puissance:
|
|
n{1, 2, 3,…} |
Somme d'un nombre
donné à des puissances successives
|
|
Type 2: on
étudie les propriétés additives des nombres, les
propriétés de partitions:
tel nombre est somme de puissances sous une seule forme ou sous de multiples
formes …
Voir pages
Partitions, comment s'y retrouver >>> |
|
|
N = ak + bk + ck |
Nombre en tant que partition en somme d'une puissance donné. |
|
N = 12 + 21 + 30 |
Nombre somme de nombres successifs portés à des
puissances successives. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()