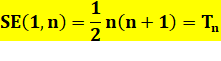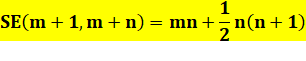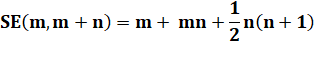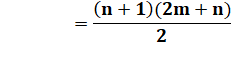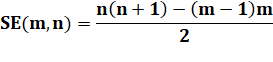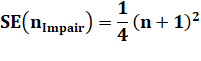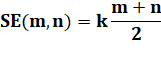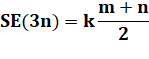|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
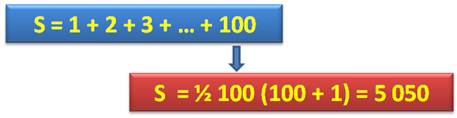
SOMME des ENTIERS consécutifs (1/2) Calcul d'une facilité déconcertante
… si on connaît le truc. On apprendra que la somme S des
nombres de 1 à n est égale à: Formule générale
Exemple
|
Voir Énigme junior / Énigme de l'entier manquant
|
|
||
|
Entiers S = 1 + 2
+ 3 + … + n |
|
|
|
S = m+1 + m+2 + …+ m+n |
Voir
Série
arithmétique |
|
|
S = m + m+1 + m+2 +
…+ m+n |
|
|
|
S = m + m+1 + m+2 + …+ n |
|
|
|
Pairs S = 2 + 4 + 6 + … + 2n
S = 2 + 4 + 6 + … + n Pair |
|
|
S = 1 + 3 + 5 + … + 2n –
1 S = 1 + 3 + 5 + … + 2n +
1 S = 1 + 3
+ 5 + … + n Impair |
|
|
Suite de k termes |
|
|
S = m + m+1 + m+2 +
…+ n k termes |
Ex: 3 + 4 + 5 + 6 = 4 (3+6) / 2 = 2 x 9 = 18 |
|
S = m + m+a + m+2a … n k termes |
Ex: 3 + 6 + 9 + 12 = 4 (3+12) / 2 = 2 x 15 = 30 |
Voir Suites
arithmétiques
Suite Sommes alternées
Quelques sommes
(classiques ou alternées)
|
Addition |
|
Somme |
|
1 + 2 + 3 + … |
+ 10 |
55 |
|
1 + 2 + 3 + … |
+ 100 |
5050 |
|
1 – 2 + 3 – 4 + … |
– 10 |
– 5 |
|
10 – 9
+ 8 – 7 + … |
– 1 |
5 |
|
1 – 2 + 3 – 4 + … |
– 100 |
– 50 |
|
100 – 99
+ 98 – 97 + … |
– 1 |
50 |
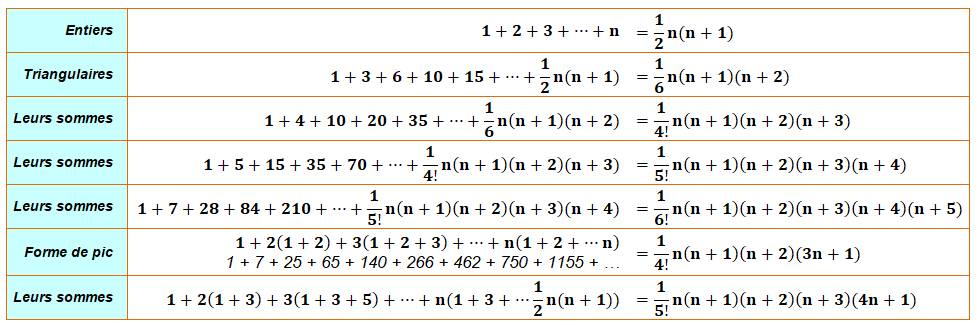
Formules connues du Chinois Zhu Shijie dans le Miroir
de jade des quatre inconnues (1303)
![]()
|
|
||
|
Voici la somme jusqu'à 9 ou
jusqu'à 10
|
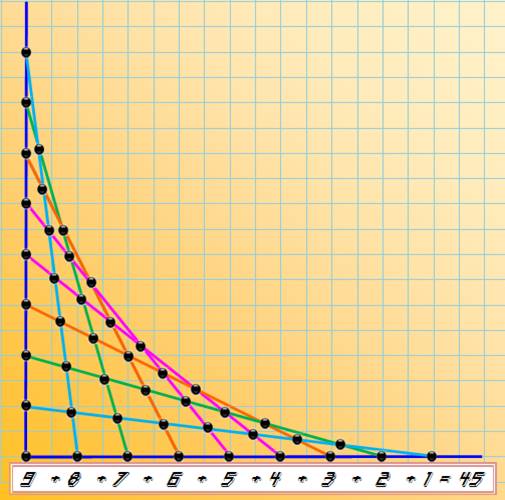
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 |
|
|
Gauss, enfant prodige
Voir Véritable
histoire |
( 1 + 100) + ( 2 + 99) + ( 3 + 98) + ... + (50 + 51)
= 101 x 50
= 5 050 |
|
|
|
x + 2x + 3x + … + 10x = 1100 x ( 1+ 2 + 3 +… + 10) = 1100 55 x = 1100 x = 20 € |
|
Voir Les cailloux du Petit
Poucet
|
Combien de petits carrés
si on construit cet escalier jusqu'au nombre 9 ? |
|
Dix
piles de 10 pièces. Toutes les pièces pèsent le même poids sauf les dix
pièces d'une pile complète qui pèsent plus ou moins 10 grammes de différence.
Comment déterminer la pile fautive et en combien de pesées sur une balance à
aiguille. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
·
La double- somme vaut
n fois n+1. ·
Et la somme cherchée la moitié de cette valeur. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||
|
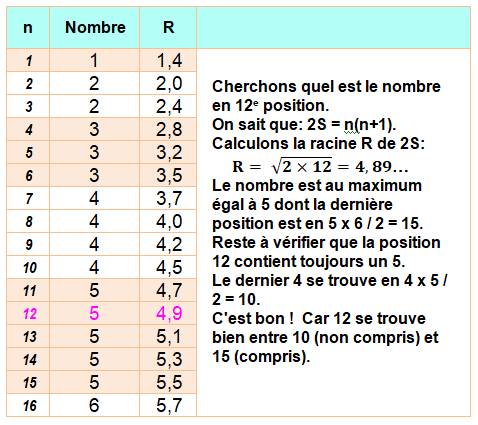
Quelques
sommes
Petite
devinette ancienne On
construit la suite des nombres de la manière suivante: 1, 2, 2, 3, 3, 3, 4,
4, 4, 4, 5 … Autant de nombres que sa valeur l'indique. Quel
est le 10e nombre, le 100e, le millionième ? Solution En
arrivant au dernier 4, par exemple, on a écrit: S = 1 + 2 + 3 + 4 = 10 nombres. La somme S des nombres de 1 à
4, laquelle est égale à n(n + 1)/2. Le dixième nombre est 4. Méthode
En
100e position Racine
de 200 = 14,14 …. C'est un nombre voisin de 14 14
x 15 / 2 = 105, le dernier nombre en 14. 13
x 14 / 2 = 91 Le 100e
chiffre est 14. En
1 000 000e position Racine
de 2 000 000 = 1414,21 …. C'est un nombre voisin de 1414 1414
x 1415 / 2 = 1 000 405, le dernier nombre en 1414. 1413
x 1415 / 2 = 998 991 Le 1 000 000e chiffre est 1414. |
||||||||||
ASTUCE pour les
puissances de 10
|
Exemples Somme
de 1 à 10 => (10/2) = 5 => répété, soit 55 Somme
de 1 à 100 => (100/2) = 50 => répété, soit 5050 Somme
de 1 à 1000 => (1000/2)= 500 => répété, soit 500500 Règle générale Somme
de 1 à 10k = 50…0k-1
50…0k-1 Prendre
la puissance de 10, la diviser par 2 et répéter ce nombre. Justification
Le
premier terme est suivi d'autant de 0 que nécessaire pour y loger le deuxième
terme (pas de retenue). |
Voir Puissance de 10
Devinette du ramassage
des melons (des cailloux)
|
Vingt melons espacés
d'un mètre sur une rangée en ligne droite. Le panier de ramassage est situé à
un mètre du premier melon de la rangée. Ils sont lourds et il faut les
ramener un par un dans le panier. Quelle est Réponse: Premier aller-retour:
2 x 1 m Deuxième: 2 x 1 x 1 m Troisième: 2 x 2 x 1 m … Vingtième: 2 x 20 x 1
m Total: L = 2 x (1 + 2 + 3 + … + 20) m
Énigme
originale d'Ozanam:
100 cailloux espacés d'une toise
(environ 2 m).
|
|
|
|
|
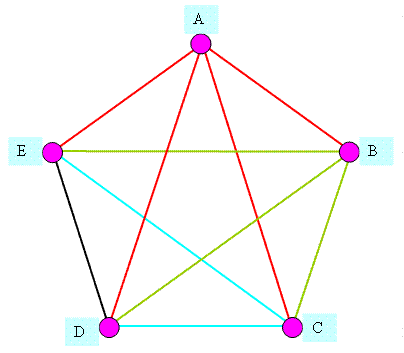
·
Dessinez 5 points, non alignés (tel que jamais 3 points
ne soient alignés). Combien de segments possibles entre ces points ? Du point A : 4 segments B : 3 C : 2 D : 1 ·
Ce qui revient à f T = ½ x 4 x 5 =
10
|
|
Débutants,
voir explication détaillée en Quantité de
segments dans un polygone / Hexagone
Souvenirs
(début des années 60)
|
Je me souviens avoir donné ce genre d'exercice comme
punition lorsque j'étais pion. Mais il y eut un inconvénient majeur! Une fois la solution connue, les
étudiants enthousiasmés m'ont redemandé d'autres trucs comme celui-ci. Ce que
j'ai fait, bien volontiers. Bénéfice: j'avais gagné leur
attention, et le calme dans l'étude et le dortoir … Et peut-être la naissance d'une vocation
pour certains d'entre eux … |
|
|
|
|
La quantité maximale de points
d'intersection obtenue avec dix lignes droites qui se croisent est égale à la
somme des nombres de 1 à 9, soit 9 x 10 / 2 = 45. Illustration
avec la technique des fils tendus
Note: la programmation du dessin des fils tendus
reste un excellent exercice d'entrainement pour débutant en programmation. Le
rendu à l'écran est immédiatement gratifiant. Faciele à réaliser avec Scratch. |
|
|
|
||
|
Histoire Karl Friedrich Gauss (1777-1855) n'était pas un petit génie,
mais un très grand génie. L'anecdote courante de la somme de 1 à 100 est une
simplification que la légende a retenue. En fait, le problème posé par le
professeur Büttner était nettement plus déroutant pour l'élève moyen. Voici le problème originel posé pour avoir
la paix dans la classe. Gauss avait bien 10 ans. Non seulement, il donne sa
réponse immédiatement. Une heure se passe, lui les bras croisés et les autres
continuant à calculer. Finalement, seule son ardoise montre le bon résultat. |
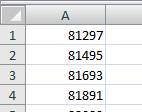
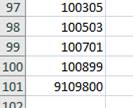
Additionnez les cent nombres suivants: 81 297 + 81 495 + 81 693 + … à chaque fois, il faut ajouter 198. La réponse est 9 109 800. Voir
Calcul ci-dessous Versions trouvées dans
la littérature Laquelle est la vraie?
Mystère! 1 + 2 + … 100 176 + 195 + …+ 2057 5 192 + 5229 + … + 8792 81 297 + 81 495 + … + 100 899 |
|
|
Méthode de la progression arithmétique |
S = a.n + ½ r.n (n – 1) |
S = 81 297 x 100 + ½ 198 x 100 x 99 = 8 129 700 +
980 100 = 9 109 800 |
|
|
Méthode du tableur |
Inscrivez les deux premiers nombres en A1 et A2. Sélectionnez ces deux cases et tirez la poignée en bas
à droite jusqu'à la 100e ligne. En ligne 101, faire la somme ( La réponse est immédiate. |
…
|
|
|
Méthode à la Gauss |
Premier
terme Pour
atteindre le 100e (99 intervalles) Centième
terme Somme
du 1er et du 100e Cent
fois cette somme La
moitié de cette double somme |
81 297 99 x 198 = 19 602 100 899 182 196 1 8219 600 9 109 800 |
|
Anglais: Gauss Schoolroom
Anecdote
Source: La vie secrète des nombres – Joaquim
Navarro – Le monde est mathématique – 2013 – Pages 19 et 20
Voir Recueil de textes
décrivant cette anecdote / Statistiques
sur citations de l'une ou l'autre des versions
Actualité de juillet
2017
|
Mathématicienne iranienne et médaille Fields, meurt à 40 ans,
suite à un cancer du sein. Elle s'est passionnée pour les maths grâce à son frère,
qui lui a transmis un livre racontant l'histoire de Friedrich Gauss, qui
permet de faire la somme des nombres entiers de 1 à 100. |
|
C'est
la somme des nombres de 1 à 9. 1
+ 2 + 3 + … + 9 = 9 x 10 / 2 = 45. |
|
Énigme Dix
piles de 10 pièces. Toutes les pièces pèsent le même poids sauf les dix
pièces d'une pile complète qui pèsent plus ou moins 10 grammes de différence.
Comment déterminer la pile fautive et en combien de pesées sur une balance à
aiguille. Solition Prendre
une pièce de la pile n°1, deux de la pile n°2, etc. Soit
1 + 2 + 3 … + 10 = 55 pièces. Si
toutes les pièces étaient normales, elles pèseraient 55p (p le poids de la
pièce normale). Si
la pile n°1 est fautive, la mesure de poids
donnera 55p + 10g, si c'est la pile n°2, elle donnera 55p + 20g. Le
supplément de poids indique directement la pile fautive. |
Voir Le sac de pièces
|
|
|
|
Se référer aux liens suivants: · Somme de 1 à 100 = 5050 Méthode de calcul utilisée par Gauss enfant · Démonstration par récurrence · Somme des entiers, carrés, cubes … Démonstration · Quantité de traits (segments) dans
un polygone · Quantité de régions dans un
cercle avec n cordes · Somme 1 + 2 + 3 + … = 1/12 (?) Voir utilisation dans les Carrés
Magiques Voir Division
des factorielles par la somme des entiers |
|
![]()
|
Retour |
·
Sommes des
entiers – Approche |
|
Suite |
·
Somme des entiers: page 2/2 ·
Sommes
alternées des entiers ·
Somme
des entiers = -1/12 ? |
|
Aussi |
·
Sommes particulières de
consécutifs ·
Somme des chiffres de 0 à 99 |
|
Voir |
·
Gauss ·
Jeux ·
Quantité
de segments dans un polygone |
|
Cette page |