|
Édition du: 07/08/2023 |
|
INDEX |
Types de Nombres – Polynômes |
|
|
Cunningham – Généralisés |
Cunningham – Simples |
|
![]()
|
Cunningham généralisés ou Nombres binomiaux Nombres
binomiaux (deux termes) égaux à la somme de deux puissances. Ils peuvent être
simplifiés avec le second terme égal à 1. Ils peuvent être
particularisés en nombres
de Mersenne ou nombres de
Fermat. |
||
|
|
Sommaire de cette page >>> Approche >>> Définition et notation >>> Factorisation |
Débutants Glossaire |
|
Mathématicien
britannique né à Dehli (Inde). Archéologue,
militaire puis mathématicien expert en théorie des nombres. Notamment:
recherche des facteurs des grands nombres de la forme: Le
projet Cunningham, commencé en 1925 avec Woodall est toujours d'actualité. Il
vise à recenser la décomposition en facteurs premiers des nombres de
Cunningham (simples) pour b = 2, 3, 5, 6, 7, 10, 11, 12 et n très grand. |
Voir Contemporains
|
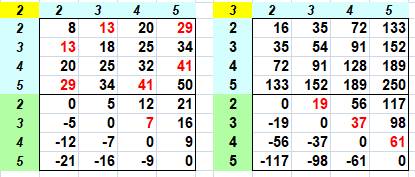
Table des premiers
nombres binomiaux pour n
= 2 et n = 3 (sans le "1"). Lignes 2 à 5: nombres C+ = bn + an,
comme 3² + 2² = 9 + 4 = 13 Lignes 6 à 9: nombres C- = bn – an,
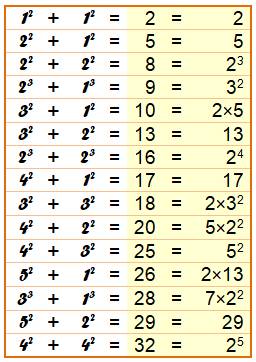
comme 3² – 2² = 9 – 4 = 5 En rouge, les nombre premiers. Table des premiers
nombres binomiaux dans l'ordre croissant de 2 à 32 avec leur factorisation. Avec le second terme égal à 1, ce sont les Cunningham simples. Ces nombres sont très nombreux: dense et en
nombre infini. Avec eux, on s'intéresse à la factorisation,
comme 4² + 2² = 20 = 5 x 2². Cunningham et d'autres mathématiciens comme
Woodall ont étudié cette factorisation pour les très grands nombres. |
Suite de la table >>> |
|
|
Les nombres de Cunningham généralisés ou nombres
binomiaux sont du type binomial (somme algébrique de deux termes). Les nombres b, a et n sont des nombres entiers
positifs avec n > 1. |
|
|
|
Cas des C- Pour tout n |
175 – 105 est divisible par 7, en effet: = (17 – 10)(174
+ 173x10 + 172x102 + 17x103 + 104) = 7 x 188 551 =
1 319 857 |
|
|
Pour n.m (n et m >0) |
176 – 106 est divisible par 7 |
|
|
Cas des C+ Pour n impair |
175 + 105 est divisible par 27, en effet: = (17 + 10) (174
– 173x10 + 172x102 – 17x103 + 104) = 27 x 56 291 =
1 519 857 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |