|
||||||||||||||||||||
![]()
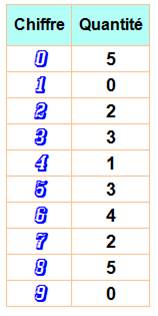
Le plus grand nombre polydivisible
|
Ce
nombre de 25 chiffres est divisible par 25; Sans
le 5 des unités, il est divisible par 24; Sans
le 25, il est divisible par 23; Etc. |
Voir Divisible
résistant
|
Noms |
NOMBRES POLYDIVISIBLES Nombre magiques |
|
|
Famille |
Nombre / |
|
|
Approche |
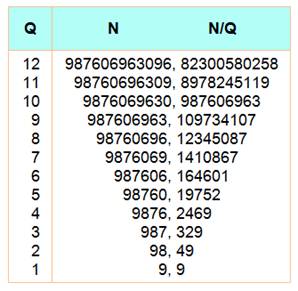
Ce nombre de 12 chiffres est divisible par 12. Tronqué de son unité, il est divisible par 11. Encore un chiffre en moins et il est divisible
par 10. Etc. Ce nombre est le plus grand nombre de 12 chiffres
ayant une telle propriété |
|
|
Définitions |
Définition formelle Nombre
tels que
Définition récursive (qui utilise sa propre définition pour se définir) Un nombre
est polydivisible (ou magique) s'il est divisible par sa quantité de chiffres
et si ce nombre tronqué de son unité est aussi polydivisible. Par définition,
les nombres de 0 à 9 sont polydivisibles. |
|
Voir Récursivité
|
|
||
|
1 chiffre Tous les
nombres à un chiffre. |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
|
|
2 chiffres Tous les
nombres pairs. |
10, 12, 14, 16, … 96, 98 |
|
|
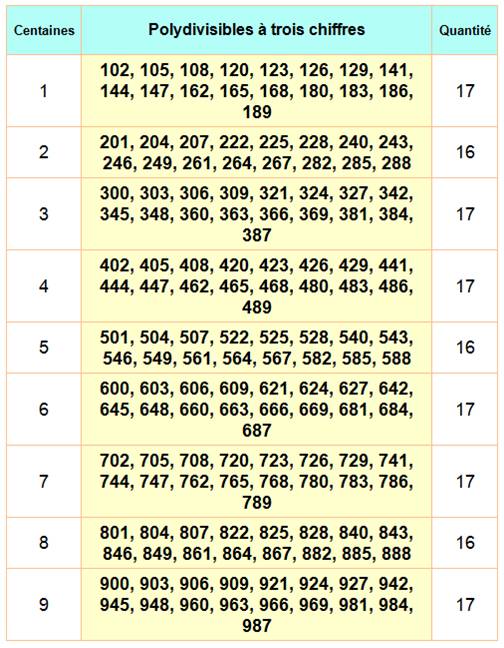
3 chiffres Il y en a
150. Du plus
petit 102 Le nombre
987 est effectivement divisible par 3, et le nombre 98 par 2. |
|
|
|
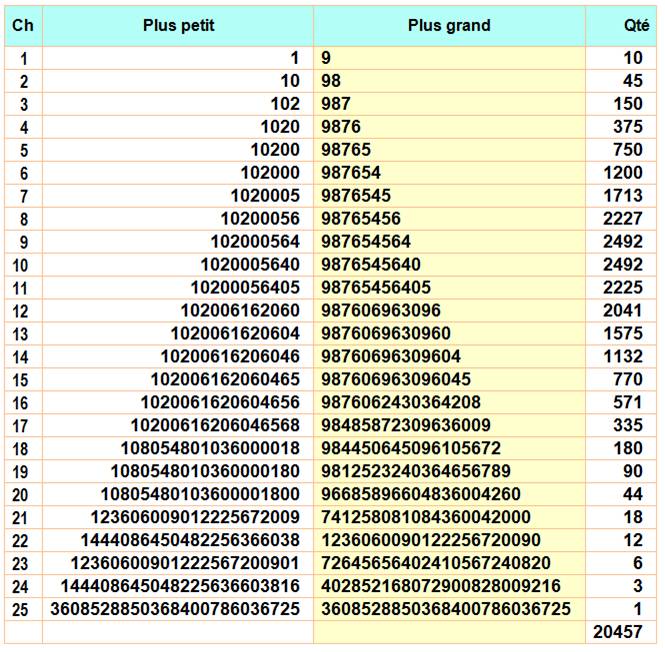
k chiffres Il existe seulement 20 547 nombres
polydivisibles Le dernier est le seul à 25
chiffres: 3 608 528 850 368 400 786
036 725 = 3,608 … 1024 Voir Statistiques ci-dessous. |
||
|
Le
nombre 381 654 729 est le seul polydivisible qui est formé avec tous les
chiffres de 1 à 9. Voir
ce nombre pannumérique.
|
|
|
|
|
Les derniers Pour 24 chiffres le nombre
intermédiaire est: 360852885036840078603672 Pour 23 chiffres, les six
représentants sont: 12360600901222567200901,
14440864504822563660381, 24085888200010566020746, 36085288503684007860367,
40285216807290082800921, 72645656402410567240820. |
|
|
|
||
|
Principe Cette programmation exige un peu d'habitude. Il s'agit d'imbriquer
trois boucles d'analyse: une pour la quantité de chiffres, une autre pour
examiner les nombres d'une liste en cours et la troisième pour ajouter un des
chiffres de 0 à 9 à chacun des nombre à examiner. Le programme utilise la facilité de concaténation du logiciel Maple. Cette "astuce"
permet d'indicer une liste ou un ensemble avec un numéro évolutif. |
||
|
Programme
|
Commentaires Initialisation et indication de la quantité de
chiffres à examiner en qmax. P est l'ensemble
des nombres polydivisibles. Le premier (P1) est initialisé avec les nombres
de 1 à 9. Boucle en d (comme diviseur) pour examiner les
nombres à d chiffres qui doivent être divisibles par d. P "double barre"
d est lu par le programme comme Pd (ensemble P de numéro d). La double barre
est l'opérateur de concaténation. Boucle en n pour l'examen de chaque nombre
jusqu'au dernier de l'ensemble précédent (calculé avec nops). Boucle en ch pour balayer les 10 chiffres à
ajouter comme unité du nombre n en
cours d'examen => N = 10n + ch Si ce nombre est divisible par d (N mod d = 0),
on l'ajoute à l'ensemble Pd. Fin des trois boucles. Le programme est
alors en possession de qmax ensembles de nombres polydivisibles. On peut les imprimer indépendamment ou tous à la
suite en opérant l'union de ces ensembles. L'opérateur 'union' s'applique aux arguments qui
le suivent. Ici, d'abord l'ensemble contenant le nombre 0, puis une séquence
appelant tous les ensembles calculés de 1 à qmax. Le nops en fin de programme permet de donner la
quantité de nombres polydivisibles trouvés. En bleu, début d'impression. En posant qmax := 25, on trouve les 20 257
nombres polydivisibles. |
|
Voir Programmation
– Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Polydivi.htm |
![]()