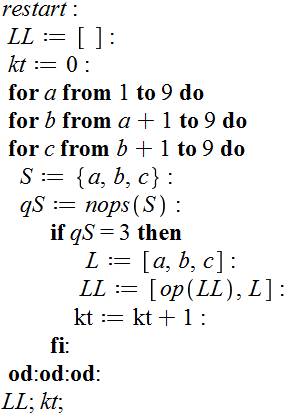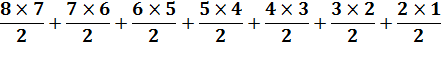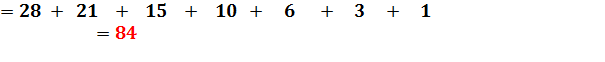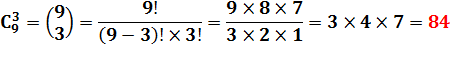|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite de NOMBRES Test de redondance Manipulation des ensembles Pour tester si la suite de
nombres entiers (a, b, c, d …) contient des nombres identiques (redondants) on
peut tester les nombres deux à deux. C'est fastidieux, surtout s'il y a
beaucoup de nombres dans la suite. Une méthode plus rapide
consiste à utiliser la notion d'ensemble Avec Maple:
|
|
|
||
|
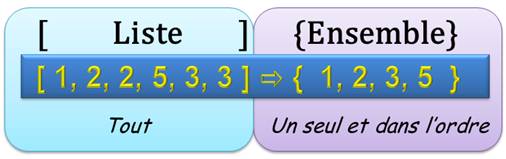
Notre but Montrer comment
Maple permet de supprimer les doublons dans une liste de nombres. Une liste est définie simplement en plaçant les nombres
entre crochets. En mettant des accolades, Maple comprend qu'il s'agit d'un ensemble (anglais: set) et
ne conserve qu'un nombre de chaque type. En plus, il les restitue du plus
petit au plus grand. En bref
|
||
|
Exemple – Approche
|
Restart pour redémarrer, réinitialiser. Définition de la liste A (crochets). Définition de l'ensemble SA (accolades). Impression
de la liste et de l'ensemble. ('A' permet
d'imprime le A en tant que lettre). Définition de la liste B. Définition de l'ensemble SB. Impression de la liste et de l'ensemble. Pour A, les deux sorties sont identiques, car
tous les nombres sont différents Pour B, la liste présente des doublons qui ont
été éliminés dans la sortie de l'ensemble. |
|
|
Amélioration
|
But: transformation automatique des listes en
ensembles par l'instruction "op". SA =
{ } pour signifier que SA est défini
comme un ensemble. op(A) pour sortir la liste A de ses crochets. Notez que l'ensemble élimine les doublons et ordonne les nombres. |
|
|
|
|||
|
Notre but Nous souhaitons
obtenir toutes les suite de trois chiffres (Ex: 1,
2, 3) sans répétition de chiffres (Ex: 1, 1, 2). Nous souhaitons également
éliminer les configurations équivalentes
(Ex: 1, 2, 3 et 3, 1, 2). En un mot:
énumérer les combinaisons de trois
chiffres parmi 9 et les compter. |
|||
|
Programme
|
LL est une liste vide (on dit: déclaration de
liste). Un
compteur (kt) est initialisé à 0. Trois
boucles avec a de 1 à 9; b ne repasse pas sur ce qui a été vu
par a et commence donc à a + 1; itou pour c. L'ensemble
(S) des trois nombres courants est formé. qS est la
quantité d'éléments dans S. Il n'est
égal à 3 que si les trois nombres a, b et c sont différents. Dans ce cas:
traitement de la liste sans répétition (if). L est la
liste des trois nombres. LL (longue liste) enregistre toutes les listes
valides: concaténation de la longue liste existante (op(LL))
avec la liste (L) qui vient d'être trouvée. Le
compteur kt est incrémenté. Fin du
traitement de liste sans répétition (fi). Fin des
trois boucles (od). Impression
de la longue liste et du compteur. Rappel: le
point-virgule impose l'impression. |
||
|
Sortie du programme
Observez la mise en tableau de 12 x 7 = 84. |
La longue liste énumère tous les cas de trois
chiffres différents Le compteur en comptabilise 84. pouvons-nous
nous assurer du résultat? En prenant 12, le chiffres suivant va de 3 à 9, soit 7 cas; pour 13,
le chiffre suivant va de 4 à 9 soit 6 cas; puis 5, 4, 3, 2 et 1 cas. Au
total, avec 1 suivi de deux chiffres, il ya : 7 + 6 + … + 1 = 7 x 8 / 2 = 28
cas En prenant 23, le chiffre suivant va de 4 à 9, soit 6 cas; etc. Soit 6
x 7 /2 = 21 En prenant 34, 5 x 6 / 2 = 15 |
||
|
Bilan
Rappels Quantité de combinaisons de 3 chiffres parmi 9 (avec les deux notations possibles):
Quantité de nombres de 3 chiffres: 729 = 93 (Ex: 111, 112, 113 …) Quantité de permutations des chiffres de 1 à 9 : 362 880 = 9! (Ex: 132654897) |
|||
Voir Combinatoire
|
|
|||
|
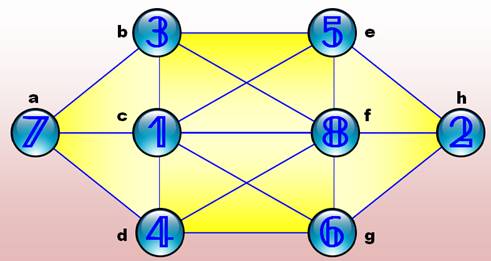
Sur ce graphe, les chiffres de 1
à 8 sont placés de sorte qu'aucun ne côtoie son voisin immédiat. Ex: le 1
n'est pas relié au 2. Nous nous
proposons de vérifier s'il s'agit de la seule solution. |
|
||
|
Programme
|
Lancement de quatre boucles avec a, b, c, et d. Vérification si l'ensemble comporte 4 éléments,
auquel cas a, b, c et d sont bien différents. Un premier test à ce niveau
permet de limiter le travail ultérieur pour des configurations non
recevables. Lancement de quatre boucles avec e, f, g et h. Vérification si l'ensemble comporte 8 éléments,
auquel cas les huit nombres sont bien différents. Test de proximité: comme a – b en valeur absolu
doit être différent de 1. Tous les cas de proximité sont proscrits (AND qui
est la fonction logique ET) Les huit nombres sont différents et les
conditions de proximité sont réunies, alors, on imprime les huit nombres (lprint). Fin des conditions (fi) et des bouches (od). |
||
|
Impression du résultat
|
Ces quatre configurations sont identiques par symétrie. C'est la n°3 qui
est représentée. La configuration proposée aux symétries près est unique. |
||
![]()
|
Retour |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
![]()