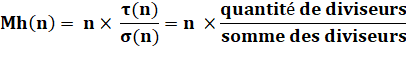NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de nombres
Débutants Général	COMPOSÉS			Glossaire Général
INDEX Types de nombres	Composés	Sphéniques	Harmoniques
		Sommaire de cette page >>> Caractéristiques >>> Liste >>> Nombres d’ORE – Programme >>> Moyenne harmonique du totient: un entier

NOMBRES à moyenne harmonique entière

ou nombre d'Ore

Nombres dont la moyenne harmonique de ses diviseurs est un nombre entier.

Caractéristiques
Famille	Nombre / Diviseurs / Multiplicatif / Composé
Définitions	Nombres dont la moyenne harmonique de ses diviseurs est un nombre entier.
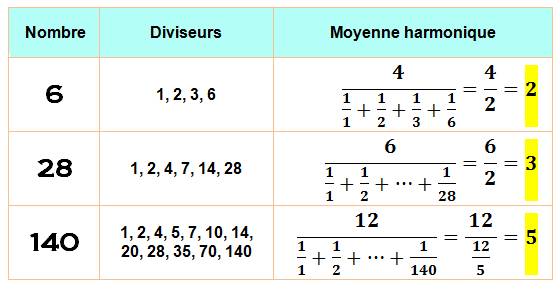
Exemples
Origine	Nombres définis par Oystein Ore en 1948.
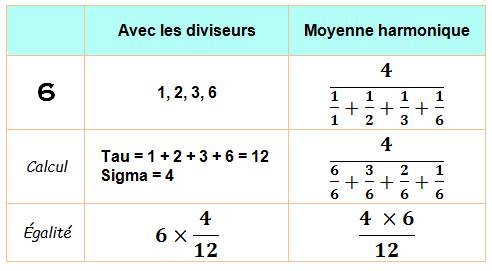
Relation	Exemple montrant la logique de l'égalité Voir Réduction au même dénominateur
Propriétés	Tous les nombres parfaits sont harmoniques. Il semblerait que seul 1 est un harmonique impair.
Anglais	Harmonic divisor numbers

Voir Fonctions arithmétiques

Liste
Pour n de 1 à 1 000 000 En rouge les nombres parfaits.	1, 6, 28, 140, 270, 496, 672, 1 638, 2 970, 6 200, 8 128, 8 190, 18 600, 18 620, 27 846, 30 240, 32 760, 55 860, 105 664, 117 800, 167 400, 173 600, 237 510, 242 060, 332 640, 360 360, 539 400, 695 520, 726 180, 753 480, 950 976.

Nombres d’ORE – Programme
Programme Maxima	Commentaires La fonction Ore indique si le nombre n est un nombre d’Ore (T=1) ou non (T=0). La liste des diviseurs est en D. La somme des inverses des diviseurs est en Sid. La moyenne harmonique des diviseurs est en Mh. Si cette moyenne est un entier (integerp) le témoin T est mis à 1. Le programme principal ouvre une liste L et explore les valeurs de n de 1 à 1000 (par exemple). Résultats du traitement sous forme d’une liste L.

Voir Programmation – Index

Moyenne harmonique du totient: un entier
Exemple avec n = 2022 Son totient: Phi = 672 est harmonique On peut aussi se reporter à la liste des nombres harmoniques, ci-dessus.		Diviseurs de 672 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 32, 42, 48, 56, 84, 96, 112, 168, 224, 336, 672 Moyenne harmonique des diviseurs: h = 8
Liste (n)	1, 2, 7, 9, 14, 18, 29, 58, 213, 271, 284, 426, 542, 673, 731, 791, 833, 1011, 1015, 1017, 1131, 1305, 1346, 1348, 1376, 1462, 1508, 1568, 1582, 1624, 1666, 1720, 1960, 2022, 2030, 2034, 2064, 2088, 2262, 2352, 2436, 2580, 2610, 2940, 2971, 5942, 7775, 8191, 8653, …
Liste [n, h]	[1, 1], [2, 1], [7, 2], [9, 2], [14, 2], [18, 2], [29, 3], [58, 3], [213, 5], [271, 6], [284, 5], [426, 5], [542, 6], [673, 8], [731, 8], [791, 8], [833, 8], [1011, 8], [1015, 8], [1017, 8], [1131, 8], [1305, 8], [1346, 8], [1348, 8], [1376, 8], [1462, 8], [1508, 8], [1568, 8], [1582, 8], [1624, 8], [1666, 8], [1720, 8], [1960, 8], [2022, 8], [2030, 8], [2034, 8], [2064, 8], [2088, 8], [2262, 8], [2352, 8], [2436, 8], [2580, 8], [2610, 8], [2940, 8], [2971, 11], [5942, 11], [7775, 10], [8191, 15], [8653, 7], …

Suite	Nombres homogènes Nombres multiparfaits harmoniques
Voir	Moyenne harmonique Suite harmonique
Site	Nombre à moyenne harmonique entière – Wikipédia Harmonic Divisor Number – Wolfram MathWorld OEIS 001599 - Harmonic or Ore numbers: numbers n such that harmonic mean of divisors of n is an integer.
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/Harmoniq.htm