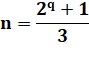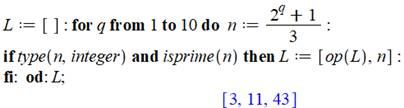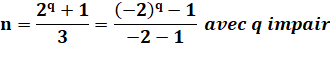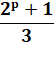Nombres premiers de Wagstaff

Édition du: 12/02/2024

M'écrire

Brèves de Maths

INDEX

Types de nombres

Mersenne & cousins

Nombres de Fermat

Nombres de Mersenne

Nombres de Wagstaff

Carol et Kynea

Compagnons

Faites un double-clic pour un retour en haut de page

NOMBRES de WAGSTAFF

Nouvelle conjecture de Mersenne

Nombres qui, comme les nombres de Mersenne, font intervenir une puissance de 2, et qui ont des propriétés notables face aux nombres premiers.

Samuel Wagstaff est un mathématicien et informaticien américain né en 1945. Expert notamment en algorithmique de factorisation des nombres. Il a longtemps tenu à jour une liste de très grands nombres factorisés. Application en cryptographie.

Comme à mon habitude, cette page est une introduction aux nombres de Wagstaff. Un sujet de recherches pointues. Toute imprécision serait de mon fait. Merci à M. Tony Reix pour ses conseils et commentaires.

Sommaire de cette page

>>> Définition

>>> Propriétés

>>> Records

Débutants

Nombres

Glossaire

Nombres

Intérêt

L'intérêt essentiel que je vois dans les nombres de Wagstaff, c'est que, alors qu'ils ne sont pas (comme les nombres de Mersenne ou Fermat) sous la forme N+1 ou N-1 (ce qui permet d'utiliser des propriétés profondes mathématiques), ils leur sont très proches (puissances de 2 aussi), et que les méthodes classiques utilisées pour prouver qu'un nombre de Fermat ou Mersenne est premier fonctionnent aussi pour trouver des nombres de Wagstaff NPP (si Wq est premier, alors il est prouvé qu'on a un algorithme qui fonctionne. Bref, il y a l'espoir de trouver une méthode de preuve pour ces nombres particulier.

Tony Reix

Définition		haut
Nombres de Wagstaff Ce sont les nombres rationnels de la forme: Liste pour q de 0 à 10 2/3, 1, 5/3, 3, 17/3, 11, 65/3, 43, 257/3, 171, 1025/3.	Nombres PREMIERS de Wagstaff Ce sont les nombres entiers de Wagstaff qui sont premiers. Alors q est premier impair, ce qui assure que n est entier lors de la division par 3. Liste pour q de 0 à 100 3, 11, 43, 683, 2731, 43691, 174763, 2796203, 715827883, 2932031007403, 768614336404564651, 201487636602438195784363. Il en existe 34 connus en 2023 (Source Tony Reix). OEIS A000978 et OEIS A000979
Programmation Maple Programme de recherche simple, applicable pour les "petits" nombres. (10 secondes pour q = 5000 avec 23 premiers de Wagstaff trouvés, le dernier ayant 1064 chiffres).

Propriétés

haut

Propriété de q

Si le nombre de Wagstaff est premier, alors l'entier q est nécessairement premier, donc impair (note pour q = 2, le nombre n'est pas premier).

Primalité

Il n'existe pas de test de primalité analogue à celui de Lucas-Lehmer pour les nombres de Wagstaff.

En revanche, on sait trouver rapidement des nombres de Wagstaff probablement premiers (NPP).

Les tests utilisés pour trouver des NPP de Wagstaff utilisent différentes méthodes ressemblant au test de Lucas-Lehmer (LLT) pour les nombres de Mersenne ou aussi au test de Pépin pour les nombres de Fermat,

Tony Reix montre que la méthode (prouvée ) de Denomme/Savin - Tsumura à base de courbes elliptiques pour prouver qu'un nombre de Fermat est premier fonctionne expérimentalement aussi pour les nombres de Wagstaff. Mais il n'y a pas de démonstration mathématique que, si le nombre de Wagstaff est premier, alors l'algorithme fonctionne. Bref, cette méthode n'a pas été prouvée pour permettre de trouver des NPP de Wagstaff, même si la vérification a été poussée très loin.

Commentaire deTony Reix

Forme

Un nombre premier de Wagstaff peut aussi être interprété comme un repunit en base -2:

Conjecture dite:

Nouvelle conjecture de Mersenne (1989)

Conjecture de Bateman, Selfridge, et Wagstaff

Soit p un nombre impair quelconque, si deux de ces conditions sont remplies alors la troisième l'est:

Conjecture vérifiée pour p < 10⁷.

On ne connait que neuf nombres satisfaisant les trois conditions à la fois:
3, 5, 7, 13, 17, 19, 31, 61, 127. On pense que la liste est complète.

Cette conjecture serait alors un nouvel exemple de la loi de Guy sur les petits nombres.

Référence OEIS: A122834 / A000043 / A000978 / A107360 A120334

Records			haut
Premier	Le plus grand nombre premier de Wagstaff connu en 2015 et en 2023:	q = 83 339 q = 138 937
Probable premier	Le plus grand nombre probablement premier (NPP) de Wagsaff. Découvert par Tony Reix en 2010:	q = 4 031 399
	En 2013, Ryan Proper annonce deux nouveaux NPP de Wagstaff:	q = 13 347 311 q = 13 372 531

Wagstaff - PrimePages – Tenue à jour des records

Merci à Tony Reix, expert et auteur de recherches sur ces nombres

Haut de page (ou double-clic)

Retour	Nombres de Mersenne
Suite	Mersenne – Suite Mersenne composés Mersenne – Table des nombres et records Mersenne généralisés Fermat Nombres sublimes
Voir	Carrés Magiques Géométrie – Index Humour – Index Jeux – Index Nombres magiques Rubriques débutants Théorie des nombres Tous les types de premiers
Sites	Nombre premier de Wagstaff – Wikipédia New Mersenne prime conjecture – The Prime Glossary Wagstaff prime – Wolfram MathWorld Wagstaff primes – Rosetta code – Programmation notamment en Python An Efficient Probable Prime Test for Numbers of the Form – Renaud LIFCHITZ & Henri LIFCHITZ A new proprety of Mersenne numbers- Tony Reix A LLT-like test for Mersenne numbers, based on cycles of the Digraph under x2 − 2 modulo a Mersenne prime – Tony Reix**
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/Wagstaff.htm