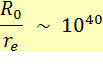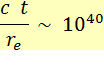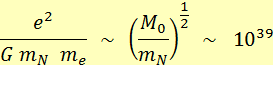NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/01/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	RUBRIQUE PHYSIQUE
Débutants Général	Constante 10 ^40	Glossaire Général
	S'écrit avec un "1" suivi de 40 zéros 10 000 000 000 000 000 000 000 000 000 000 000 000 000

Valeurs
Temps 10 ^40 =	Âge de l'Univers divisée par temps de traversée du proton par la lumière.
Longueurs 3,3 10 ^40 =	Rayon de l'Univers observable (10^26 m) divisée par rayon de l'électron (3 10^-15 m).
Forces 0,227 10 ^40 =	Intensité de la force de gravité divisée par celle de la force électromagnétique.
Particules (10 ^40 ) ² = 10 ^80 =	Quantité de protons dans l'Univers.
Masses (0,25 10 ^40 ) ² = 6 10 ^78 =	Masse de l'Univers divisée par masse du proton.
Degré de liberté 2,1 10 ^40 =	Quantité maximum de degrés de liberté dans une sphère dont le rayon est égal à la longueur d'onde de Compton du nucléon.
Calculs 3,9 10 ^41 =	Nombre maximum d'opérations logiques que pourrait effectuer un nucléon sur la durée de l'Univers.

Voir Échelle des dimensions de l'Univers

Historique
Rapport mis en évidence par	Arthur Eddington (1931) Paul Dirac (1938) Hypothèse des grands nombres de Dirac.

Gravité et force électromagnétique
Soit un bout de bois. Le haut et le bas du bâton tiennent solidement ensemble. Un coup de scie au milieu et la partie du bas tombe, attirée par la Terre.	La force qui attire le morceau coupé vers le bas est plusieurs milliards de milliards de fois plus faible que celle qui tenait les deux morceaux de bois ensemble.
Un électron et un positron à 0,2 mm de distance l'un de l'autre Calculons l'attraction gravitationnelle (A) et prenons-la comme référence.	Pour obtenir la même force électromagnétique (E = A) entre les deux particules, il faudrait les éloigner de 15 années-lumière! N'oublions pas que, en plus, la force décroît avec le carré de la distance.

Plus théorique!
M0 masse de l'Univers observable t âge de l'Univers c vitesse de la lumière R0 rayon de l'Univers observable G constante de gravitation e charge de l'électron re rayon de l'électron me masse de l'électron mN masse du nucléon

Voir	Puissance de dix
DicoNombre	Nombre 40 Nombre 10^40
Sites	The Mysterious Eddington-Dirac Number Hypothèse des grands nombres de Dirac – Wikipédia