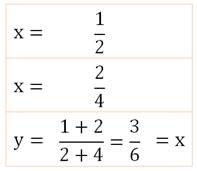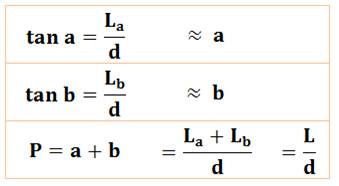|
|||||||||||||||||||||||||||||||||||
![]()
|
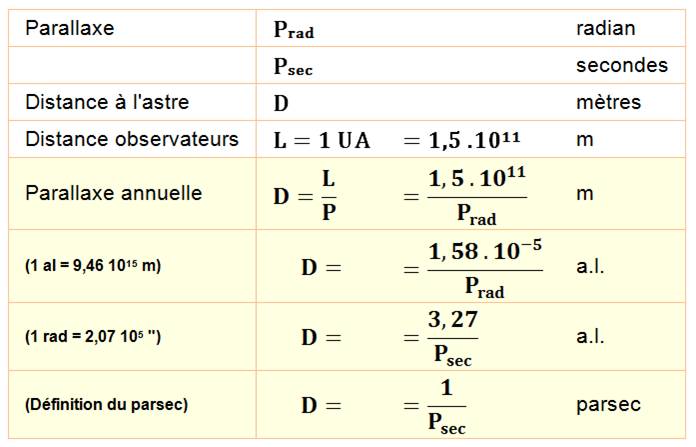
PARALLAXE
Pour les astres du système solaire: Parallaxe diurne: angle sous
lequel on voit le rayon de la Terre (P
= angle OLT). Pour les autres astres
(étoiles): Parallaxe annuelle: angle
sous lequel on voit le demi-grand axe de l'orbite terrestre. Le moyen de
connaître la distance des objets célestes. |
|
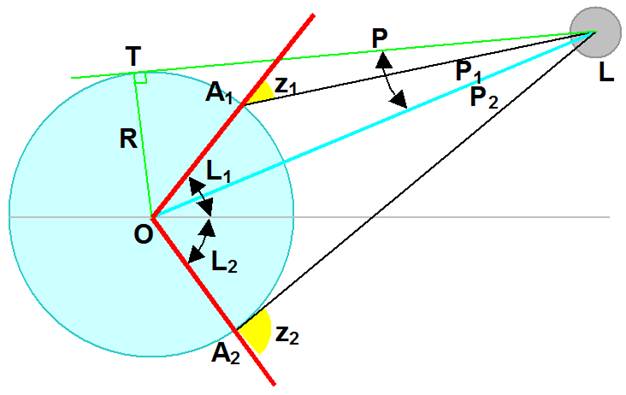
Figure
/ notations
En
mesurant les angles z1 et z2, connaissant la latitude
des lieux A1 et A2, on calcule la valeur de la
parallaxe P. |
Il est
conseillé de consulter d'abord Parallaxe - Glossaire
|
|
|||
|
Ce que l'on cherche |
Parallaxe |
Angle P = angle OLT |
|
|
Tout de suite |
Dans le triangle
rectangle
OLT |
R = OL . sin P |
|
|
|
Or, P est un petit
angle |
R » OL
. P |
|
|
(1) |
Ou (on note avec le
signe =) |
OL = R / P |
|
|
Le point de départ |
On fait deux
observations |
en A1
et en A2 |
|
|
|
Longitude |
la
même |
|
|
|
Latitude |
L1
et L2 |
|
|
|
Angles vis à vis de
la Lune |
z1
et z2 |
|
|
|
Le rayon de la
terre |
R = OA1 = OA2 |
|
|
Calcul 1 (2) |
Dans le triangle
OLA1 Avec sinus = sinus du supplémentaire |
|
|
|
Dans le triangle
OLA2 |
|
|
|
En divisant |
|
|
(3) |
En notant que les
angles P1 et P2 sont
petits |
|
|
Calcul 2 |
De (2) en
remplaçant OL (1) En pensant que P1
est petit |
|
|
|
On obtient une
première formulation de P |
|
|
|
Et symétriquement |
|
|
|
En conséquence |
|
|
Pour
se convaincre de la validité de cette dernière égalité fractionnaire:
|
|
Calcul 3 |
Que
vaut P1 + P2 |
? |
|
|
Somme
des angles dans OLA1 |
L1 + P1
+ ( |
|
|
Soit |
L1 + P1 = z1 |
|
|
Et
symétriquement |
L2 + P2 = z2 |
|
|
La
somme mise en forme |
P1 + P2 = z1 + z2
– (L1 + L2) |
|
Finalement |
|
|
|
|
|
|
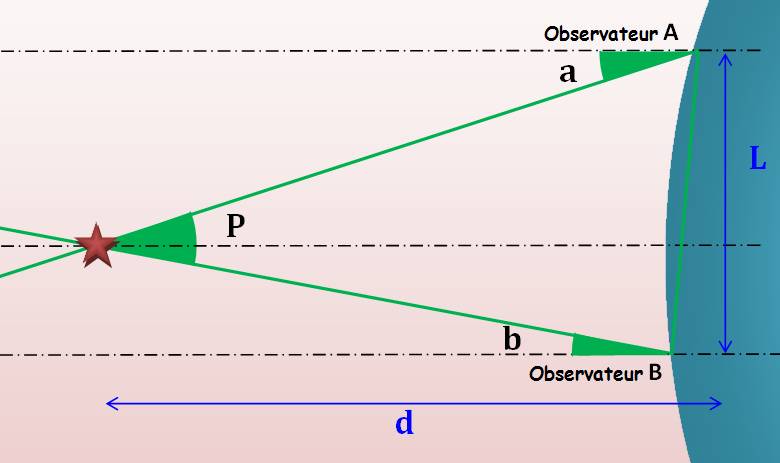
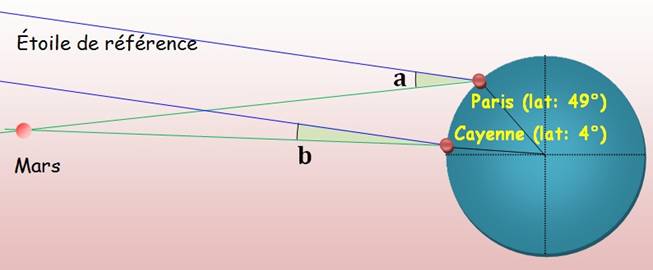
Deux observateurs positionnés en A et B, distants de L,
ou un observateur positionné d'abord en A puis en B. Compte tenu des angles alternes- internes, l'angle P
(parallaxe) est égal à la somme des angles a et b.
Nous sommes dans le cas de petits angles, on peut
approximer la tangente par l'arc. Ce qui donne les relations suivantes:
Formules
pratiques pour la parallaxe annuelle
|
|
Mars et connaissance des dimensions du système
solaire
|
En
1673, Jean-Dominique Cassini à Paris et Jean Richer en Guyane parviennent à
mesurer la parallaxe (a + b) de Mars (quelques
millièmes de degré) et en déduisent (3e lois de Kepler) la distance Terre-Soleil (UA) de l'ordre de 140 millions de km
contre près de 149,6 millions pour la valeur moyenne actuelle.
Note: la
valeur connue jusqu'alors était de 8,3 millions de km; aujourd'hui, l'unité
astronomique (distance Terre-Soleil) est connue avec la précision des radars. |
|
0, 313 " |
Première mesure de parallaxe d'une étoile
par l'astronome Friedrich Bessel en 1838. Il s'agit de 61 Cygni,
12e étoiles dans l'ordre
des distances mais invisible à l'œil nu. La parallaxe annuelle à mesurer est
à peine de 1/10 000e de
degré pour une étoile pourtant très proche (11,2 années de lumière). À cette époque, on ne connaissait pas bien
ni la distance au Soleil ni la vitesse de la lumière. De cette mesure et à partir de la
connaissance de la distance Terre-Soleil, Bessel évalue la distance à cette
étoile: 100 000 milliards de km (1014 km). Avec cette première
mesure de la distance d'une étoile, on découvre l'immensité du cosmos. |
|
|
0, 289 " |
Valeur actuelle de la parallaxe de 61 Cygni |
|
|
0, 774 " |
Parallaxe de l'étoile la plus proche: Proxima du Centaure. Donc, parallaxe la plus grande d'une
étoile. Distance déduite: 40 000 milliards de km (4
1013 km) Mesures faites également en 1938, par
Thomas Henderson (Anglais) Calcul: P = 3,27 / D = 3,27/4,22 = 0,7748 …
secondes d'arc. |
|
|
Friedrich Bessel (1784-1846) |
Allemand. Il a déterminé la position de 75 000
étoiles. |
|
Autres valeurs, voir Étoiles
|
|
||
|
Parallaxe
horizontale de la Lune |
de 52' à
62' |
|
|
Première mesure |
en 1751 par Lalande à Berlin et l'abbé La Caille au Cap |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()