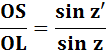|
|||||||||||||||||||||||||||||||||||
![]()
|
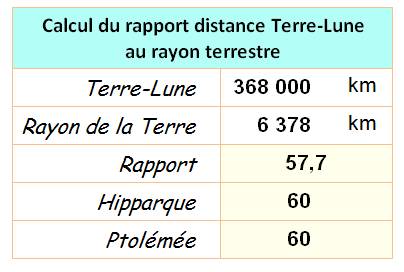
Distance
TERRE-LUNE Assez bien connue depuis Hipparque &
Ptolémée. Une histoire d'angles.
|
|
|
|
|
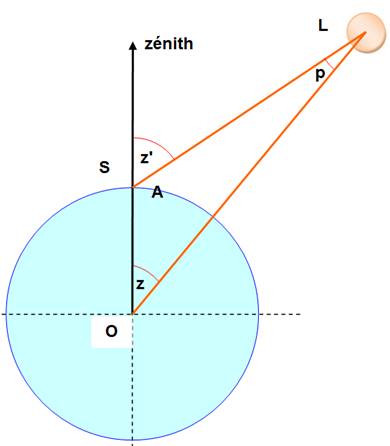
Principe Mesure de parallaxe p. Comparaison de la
distance Terre - Lune au rayon terrestre.
Voir Loi des sinus dans le
triangle Ptolémée mesure de la distance azimutale
z de la Lune au passage du méridien. Il calcule
l'angle z (selon sa propre théorie) La parallaxe est
égale à la différence. z + p + A = 180° z' + A = 180° z + p – z' = 0 p = z' – z
|
|
|
|
||
|
Lors d'une éclipse de Lune,
cet astre est dans l'axe Terre-Soleil, de l'autre côté de la Terre. Aristarque constate que la durée de
l'éclipse est d'environ 4 heures et que
|
|
|
|
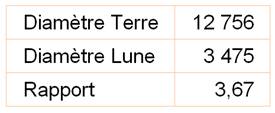
Il en déduit que le diamètre
de la Lune est quatre fois plus petit que celui de la Terre. Réalité d'aujourd'hui:
|
||
|
|
||
|
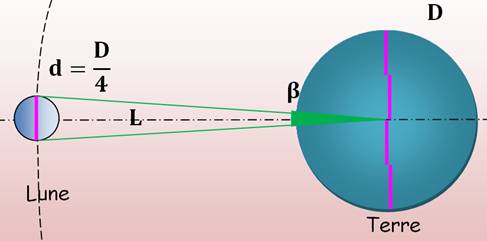
Il sait que le diamètre de
la Lune est ¼ du diamètre de la Terre. Il sait mesurer l'angle
apparent de la Lune vue de la Terre. |
|
|
|
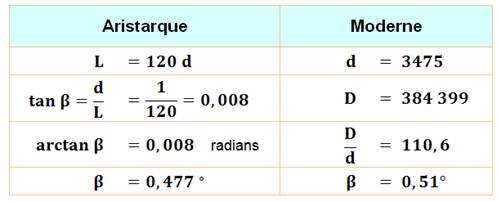
Il dessine soigneusement un
angle égal à bêta (sans doute voisin d'un demi-degré). Il place un segment
unité perpendiculairement à l'axe et mesure la longueur L. Il trouve 120. La distance
Terre-Lune est donc égale à 30 fois le diamètre de la Terre. Aujourd'hui, nous ferions le
calcul:
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()