|
|||||||||||||||||||||||||||||||||||||||||||||||
Source image: Inkscape
![]()
|
Énigme ou Paradoxe: - de la pièce qui roule, ou - du cercle qui tourne sur un autre Attention, pas si évident …
piège à l'horizon ! Extension aux mouvements des
planètes et satellites: ne pas confondre: rotation
et révolution. Pensez engrenages et vous
serez sur la bonne piste. |
Anglais: Rolling coin paradox, rolling one quarter around
another
|
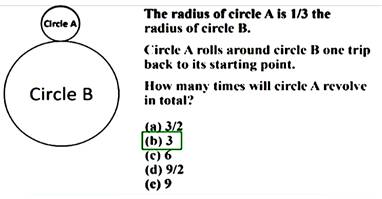
Énigme Deux cercles de
rayon R et 3R. Le petit tourne
sur le grand sans glissement. Après rotation,
il retrouve sa position de départ. Combien de tours
a-t-il effectué ? Indice Non ! ce n'est
pas trois tours … C'est la réponse
habituelle, mais elle est erronée. |
Devinette amusante et facile à réaliser
|
Au bilan, le crayon
dessine le point central et passe sur la feuille pliée qui sert à transporter
le crayon vers le cercle à dessiner.
Le tracé pour passer du centre à la circonférence existe, mais il est
au verso de la feuille. |
|
|
||
|
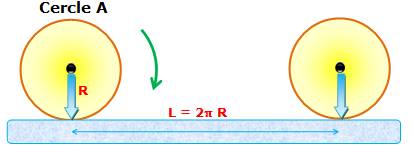
Le cercle
A roule sur la droite (ou la roue roule sur le plan) sans glisser. Elle se
retrouve dans la même position chaque fois qu'elle avance d'une longueur
égale à sa circonférence:
|
|
|
|
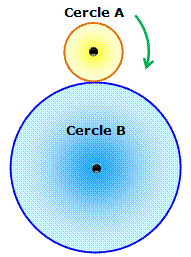
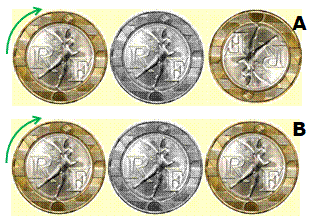
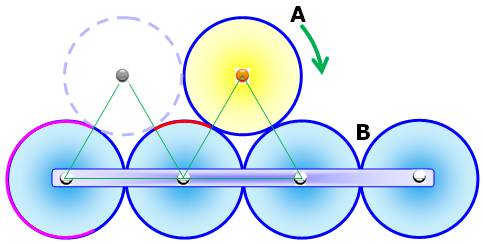
Énigme La pièce jaune roule autour de la grise. Quelle
est la bonne figure A ou B ? Réponse La figure B, celle du bas où la pièce se retrouve
dans la même situation. Faites l'expérience. La suite va expliquer pourquoi. |
|
|
|||||
|
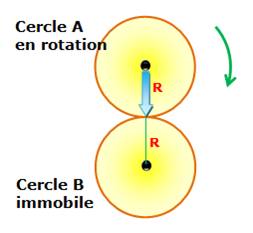
Énigme Le cercle
A roule sur le cercle B sans glisser jusqu'à se retrouver dans sa position de
départ. Le
croyez-vous ? Le cercle A effectue:
Propriété Pour se retrouver dans sa position de départ le cercle
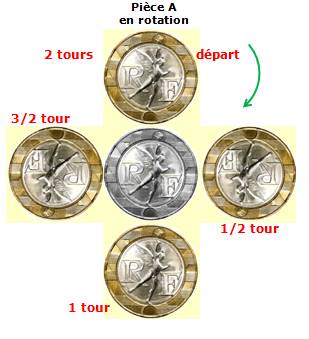
A effectue deux rotations. Explications Suivez la
pièce de 10 francs en rotation sur une autre de 10 francs. Lorsqu'elle
arrive en bas, elle a déjà effectué une rotation. Un autre est nécessaire
pour rejoindre le haut. Image des engrenages Remplaçons les deux pièces par deux engrenages de
même taille et de même quantité de dents montés sur des axes fixes. La rotation de l'un entraine la rotation de l'autre.
L'un ayant fait un tour, l'autre aussi. Soit un bilan de deux tours. Si on maintient l'un fixe, c'est
l'autre qui fait deux tours. |
Combien de tours pour A ?
Pièce de 10 francs en rotation
|
||||
|
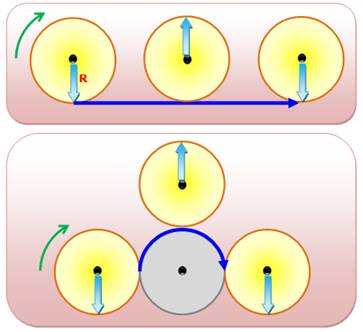
Comparaison Le trait bleu
indique le parcours pour un seul tour dans les deux cas. En haut Il y a rotation
de la pièce sur le plan. En bas Il y a rotation
de la pièce autour de la pièce grise (même chose que précédemment avec la circonférence coupée et déployée en ligne
droite) ET révolution
de la pièce jaune autour de la pièce
grise, ou tout simplement autour du point central de cette pièce grise. |
|
||||
|
Définitions Rotation: la roue tourne
autour de son propre axe. Révolution: l'objet
exécute une trajectoire circulaire ou elliptique autour d'un autre objet. Voir DicoMot
Math |
Rotation de la Terre 23,934 heures |
Révolution de la
Terre autour du Soleil 365,256 jours |
|||
|
|
||
|
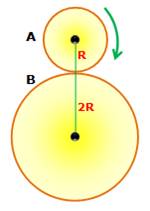
k = 2 Deux
cercles de rayon R et 2R. Le cercle A roule sans glisser sur le cercle B. Il effectue:
Le Cercle
A effectue trois tours pour retrouver sa position de départ. k général Avec deux
cercles de rayon R et k.R, le cercle A effectue (k + 1) tours. Toujours
"+ 1" tour, quelle que soit la taille du grand cercle. Cercle qui tourne à l'intérieur La
révolution s'effectue dans l'autre sens et la quantité de tours est cette
fois égale à (k – 1). |
R et 2R ⇨ 3 tours R et k.R ⇨ (k + 1) tours Avec deux engrenages: le grand ferait un tour pour k tours du plus
petit. Un total de k + 1 tours. |
|
|
|
|||
|
Lune |
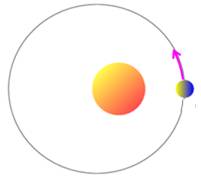
La Lune effectue sa
révolution en 27,3217 jours. Elle
présente toujours la même face à la Terre. Donc la Lune effectue une révolution et se retrouve
dans sa position initiale à la fin de ce cycle. Contrairement au cas des pièces de monnaie, elle
ne présente pas un aspect différent au fur et à mesure de sa progression. La lune se propage naturellement le long de son orbite
et semble en rotation. Nous observons là, l'effet "tout nu" de la
révolution. |
||
|
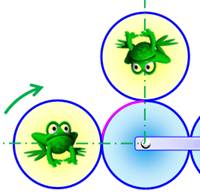
Deux tours: une
révolution + une rotation |
Un seul tour:
une révolution |
||
|
Le Soleil |
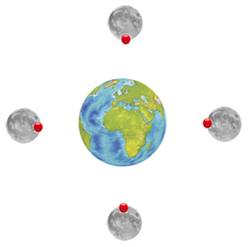
La Terre effectue sa
révolution autour du Soleil en 365
jours (et un peu
plus). La Terre
tourne sur elle-même chaque jour, soit 365 fois par an. Bilan: 365 rotations + 1 révolution = 366 tours
en un an. Le petit plus que la Terre effectue chaque jour sur son orbite
finit, au bout de l'année, à réaliser un tour. On note que cette propriété est valable, même si
l'orbite de l'astre n'est pas circulaire,
mais elliptique. |
||
|
|
||||
|
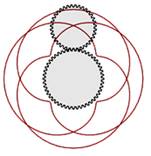
Un cercle
A roule sur un chemin formé par quatre cercles tangents en ligne. Combien
de tours exécute A pour revenir dans sa position initiale ? |
|
|||
|
Chemin de rotation du cercle A |
Le dessin montre que les centres de trois cercles
forment un triangle équilatéral (côté = 2R). L'arc rouge est intercepté par un angle de 60°. Soit
1/6 de la circonférence. L'arc en violet mesure 4/6 de la circonférence. Le chemin complet: 2 x 4/6 + 4 x 1/6 = 12/6 = 2
tours |
|||
|
Quantité de tours |
L'image des engrenages est appropriée. Une progression d'un quart de tour sur le cercle
fixe (arc
violet ci-contre) produit le double sur le cercle
mobile. Le chemin sur le dispositif B est multiplié par 2
en termes de tours effectués par le cercle mobile. Soit 4 tours. |
|
||
|
Autour d'un cercle Un
corps qui tourne k fois sur lui-même pendant qu'il effectue une révolution
complète, retrouvant son point de départ, apparaitra comme ayant effectué:
Autour de plusieurs pièces Dans
le cas d'un chemin complexe (comme dans le cas des quatre cercles), la
quantité de tours est égale au double du chemin parcouru sur le dispositif. |
![]()
|
Raisonnement incomplet En
effectuant un tour, le petit cercle progresse d'une longueur égale à sa
circonférence (2 Conclusion
(provisoire): le cercle A effectue trois tours sur lui-même. Complément, s'il vous plait Oui,
mais! Le petit cercle tourne au fur et à mesure de sa révolution autour du centre du grand cercle. Il finit par faire
un tour complet. La bonne réponse est donc: Le cercle A effectue quatre
tours sur le cercle B pour retrouver sa position de départ.
Spirographe: le cercle qui tourne autour d'un autre
fait penser aux épicycloïdes et aux jolis dessins réalisés avec un
spirographe TM.
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
![]()