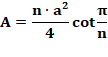|
Édition du: 23/04/2022 |
|
INDEX |
Aire des polygones |
||
Faites un double-clic pour un retour en haut de page
![]()
|
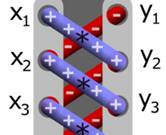
Aire du polygone avec la formule du laçage
La
formule fut établie en 1769 par Albreicht Meister (1724-1788) sur des
indications de Gauss et Jacobi. Contrairement
à la formule de Pick, elle s'applique aussi à des coordonnées irrationnelles
comme celles des polygones réguliers. Source Image wikipedia |
||
|
|
Sommaire de cette page >>> Approche avec un triangle rectangle >>> Cas d'un quadrilatère >>> Cas d'une forme polygonale >>> Cas des polygones réguliers |
Débutants Glossaire |
Anglais: Shoelace formula or
algorithm
Mots clés
Voir Lexique
|
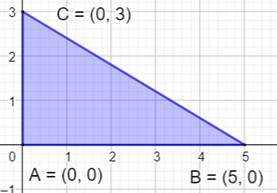
Un triangle rectangle Dans un repère orthonormé. On note les coordonnées des sommets en parcourant
le triangle dans le sens direct: Produits en croix xy et yx: le premier facteur sur la ligne de
calcul et le second sur la suivante; en bouclant pour la dernière ligne. Différence entre xy et yx. Somme de ces différences. Tableau de calculs
L'aire du triangle rectangle est égale à la
moitié de cette somme: 15 / 2 = 7,5. |
Figure
Formule de l'aire du triangle A = (xA·yB – yA·xB)
|
|||||||||||||||||||||||||||||||
Voir Brève
876
|
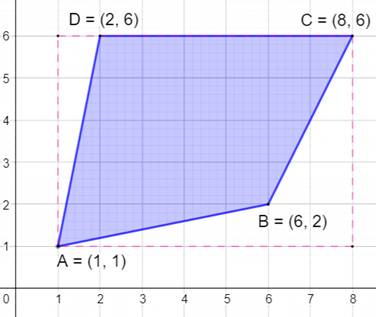
Un quadrilatère quelconque On reprend la procédure vue précédemment. Tableau de calculs
L'aire du quadrilatère est égale à
48/2 = 24 |
Figure
|
||||||||||||||||||||||||||||||||||||||
|
Pourquoi les lacets ? Le fait de prendre les produits croisés fait
penser à un procédé de laçage des chaussures (shoelace en anglais). |
|
||||||||||||||||||||||||||||||||||||||
|
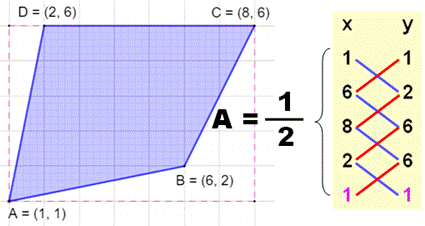
Calcul classique de l'aire du quadrilatère |
A = aire du rectangle enveloppe – (somme des triangles
et rectangles en trop autour du quadrilatère) A = 7×5 – (½ 5×1
+ 2 + ½ 2×4 + ½ 1×5) |
||||||||||||||||||||||||||||||||||||||
|
Écriture matricielle Matrice ? En fait, mise sous forme d'une suite de
tableaux 2 x 2 |
|
||||||||||||||||||||||||||||||||||||||
|
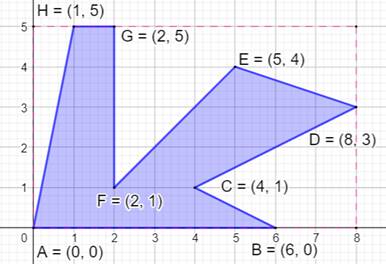
Un polygone quelconque On reprend le calcul matriciel.
|
Figure
|
||
|
Calcul classique de |
A = 8×5
– (2 + 4 + 1 + 1,5 + 6 + 4,5 + 2,5) A = 40 –
21,5 = 18,5 |
||
|
|
|
||
|
Théorème Sauf pour le carré, pour tout polygone régulier,
y compris le triangle équilatéral, les coordonnées d'au moins un sommet sont
irrationnelles. Conséquence: sauf pour le carré, la formule de
Pick est inapplicable. |
Démonstration La formule de l'aire par la méthode du laçage
montre que: L'aire d'un polygone régulier est aussi donnée
par cette
formule:
Or, la cotangente est irrationnelle pour tout n,
sauf 4. Cette contradiction prouve le théorème. |
|
Bilan
|
Que le polygone soit concave ou convexe, la
méthode du calcul de l'aire par laçage s'applique. Elle repose sur le fait que l'aire d'un triangle de
coordonnées (0, 0; a, b; c, d) est égal à la moitié du produit croisé ad –
bc. Voir Aire
du parallélogramme avec coordonnées La méthode
peut être étendue aux polygones croisés, comme aux lignes polygonales
courbes. La vidéo en référence vous montre tout cela |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |