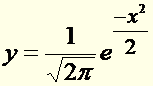NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	GRANDS ESPRITS Mathématicien
Débutants Général	GAUSS		Glossaire Général
Sommaire de cette page >>> GAUSS >>> BIOGRAPHIE >>> ŒUVRE >>> ANGLAIS

GAUSS Karl Friedrich	1777 – 1855 78 ans	Allemand Brunswick - Göttingen
Mathématicien, physicien et astronome allemand Dit le prince des mathématiciens Algèbre Géométrie Théorie des probabilités (loi de Gauss) Mais touche également à la plupart des sciences exactes et appliquées Optique géométrique Électricité Magnétisme (en coopération avec Weber) Astronomie (trajectoire des comètes) Géodésie Très méticuleux et perfectionniste, sa devise était Pauca sed matura: peu de choses, mais des choses mûres. Ses principaux élèves: Friedrich Bessel, Sophie Germain, Richard Dedekind, Bernhard Riemann.

BIOGRAPHIE

1777	0	Né à Brunswick le 30 avril. Famille pauvre et mère illettrée.
	3	Il détecte une erreur de calcul dans le dossier de son père.
	≈ 14	Il donne la formule du calcul de la somme des entiers de 1 à 100 .
1794	17	Étudie les langues anciennes. Se met aux mathématiques à l'âge de 17 ans.
1795 1798	18	Université de Göttingen.
1799	22	Thèse de doctorat: il y démontre le théorème fondamental de l’algèbre à l’aide des nombres complexes; il trouvera quatre démonstrations différentes.
1801	24	Disquisitiones arithmeticae - Traité d'arithmétique, ouvrage fondateur de la théorie des nombres, une nouvelle approche de l’arithmétique. Il introduit notamment la notion de congruence, modulo.
1804 1809	27	Sophie Germain correspond avec Gauss, d'abord sous le pseudonyme de Le Blanc, puis sous son nom véritable.
1807	30	Nommé professeur de mathématiques et directeur de l'observatoire de Göttingen, deux postes qu'il occupa jusqu'à sa mort. Considéré comme l'artisan du rayonnement de cette ville.
1827	50	Disquisitiones generales circa superficies curvas – Géométrie Traité de géométrie différentielle où Gauss étudie les surfaces et leurs courbures et leurs géodésiques. il introduit les coordonnées curvilignes, dites de Gauss.
1831	54	Définition précise des nombres complexes.
1839	62	Théorie générale du magnétisme terrestre.
1855	78	Mort le 23 février à Göttingen.

SON ŒUVRE

Théorie des nombres	Nombres Remarquablement précoce, il reconstruit seul les connaissances des Anciens.
	Division – Théorème (ou lemme) de Gauss Si d divise ab et si d et a sont premiers entre eux [pgcd(a,d) = 1], alors d divise b.
	Congruence Loi de réciprocité quadratique.
	Nombres premiers Gauss donne une formule pour la répartition des nombres premiers. Quantité de nombres premiers inférieurs à n: π(n) ≈ n / ln(n).
	Nombres complexes Représentation en tant que points du plan. Résout ainsi les équations complexes. Et donne la première démonstration du théorème fondamental de l’algèbre.

Ensemble

Théorie des ensembles Gauss est sur la piste des propriétés des anneaux et des corps, résultant de ses travaux sur les équations diophantiennes (Voir groupe).

Algèbre	Équations diophantiennes Travaux sur les équations diophantiennes (étude d'équations en nombres entiers). Équations algébriques Gauss est aussi à l'origine de la théorie des nombres algébriques, utilisée pour résoudre les équations polynomiales. Gauss démontre que: Toute équation polynomiale a au moins une solution Méthode de Gauss dite du pivot qui permet d'obtenir une matrice triangulaire. Gauss perfectionne la méthode des moindres carrés de Legendre: résolution de systèmes d'équations par approximation. Notamment, il calcule l'orbite de Cérès, découverte en 1801 par l'astronome italien Giuseppe Piazzi.
	Théorème fondamental de l'algèbre ou théorème de d'Alembert-Gauss. Gauss le démontre: La quantité de racines, réelles et complexes, d'un polynôme est égale à son degré, ou autrement formulé Tout polynôme d'une variable complexe, de degré n, admet n racines complexes (éventuellement égales)
	Constante de Gauss En 1799, il démontre que G = 0,834 …, la moyenne arithmético-géométrique de 1 et de racine de 2, vaut:
	Séries Travaux sur la convergence des séries.

Géométrie	Général Coordonnées gaussiennes caractérisant la géométrie des surfaces courbes. Premier à mettre au jour la géométrie non-euclidienne hyperbolique (courbure négative).
	Construction d'un polygone régulier de 17 côtés à la règle et au compas. Gauss trouve la solution en 1796. Il montre aussi que: La construction, à la règle et au compas, d'un polygone régulier comportant un nombre impair de côtés n'est possible que pour un nombre égal à l'un des nombres premiers 3, 5, 17, 257 ou 65 537 (nombres premiers de Fermat), ou à un produit de ces nombres.
	Problème de Gauss: combien de carrés unités peut-on placer dans un cercle de rayon entier donné ?
	Théorie des nœuds: définition du nombre d'entrelacs pour une paire de nœuds.
	Aire du pentagone convexe quelconque à partir de l'aire des triangles issus d'un sommet

Statistiques

Loi de Laplace-Gauss ou distribution de Gauss ou loi normale. Fonction de probabilités continues utilisée pour les calculs statistiques comme une approximation de nombreuses fonctions de probabilités. loi de répartition représentée par une courbe en cloche, dite fonction de Gauss ou gaussienne. Utile pour étudier les phénomènes aléatoires à causes multiples. Exemple: les bruits réels ont en général une répartition gaussienne autour d’une fréquence donnée.

Courbe de Gauss dite en cloche ou distribution normale

Voir Courbe de Gauss

Voir	Contemporains La véritable anecdote de Gauss petit Formule de calcul du jour de la semaine
Aussi	DicoMot Théorie des nombres - Index
Cette page	http://villemin.gerard.free.fr/Esprit/Gauss.htm