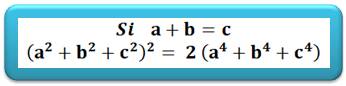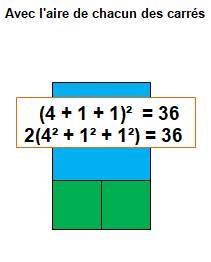|
Édition du: 11/11/2021 |
|
INDEX |
Théorème de Pythagore – Extensions |
|||
|
Pythagore en linéaire (triple quad) |
||||
![]()
|
Formule du triple QUAD Théorème de Pythagore en linéaire Une
singulière manière de voir le théorème
de Pythagore sur une droite plutôt que sur un triangle.
Notion implicite dans les travaux d'Archimède,
mais pas mentionnée par Euclide. Application
à la trigonométrie rationnelle qui procurerait un
accès plus naturel à de nombreux problèmes pratiques de géométrie
selon l'expert du domaine: N.J. Wildberger Formule du triple quad
|
||
|
|
Sommaire de cette page >>> Approche – Pythagore sur des segments >>> Formule du triple quad >>> Théorie >>> Formule du quadruple quad |
Débutants Glossaire |
Anglais: Triple quad formula
|
Construction Trois carrés, dont deux qui s'appuient sur l'un des côtés du
troisième. Dans cet exemple,
On compare les deux sommes des aires en notant a, b et c les longueurs
des côtés:
Ces deux sommes sont égales
chaque fois que a + b = c |
|
|
|
|
|
|
Voir Brève
788
|
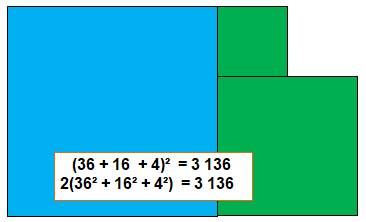
Pour démontrer la formule du triple quad, on introduit les coordonnées
de trois points sur une droite. La dimension de chaque carré (a, b ou c) est alors la différence entre les
coordonnées des sommets. |
On compare le développement des
deux expressions de part et d'autre de l'égalité. Le calcul est fastidieux. |
|
|
|
||
|
Géométrie 1D Cette propriété était connue de l'Antiquité. Aujourd'hui, elle fait
partie d'un nouveau développement des mathématiques dans le domaine de la
géométrie métrique de l'espace à une seule dimension. |
Quadrance entre deux points Formule du triple quad |
|
|
Démonstration
|
||
|
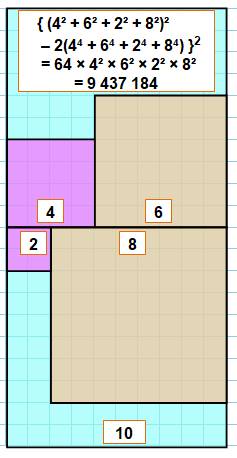
Construction Le grand carré est dupliqué, de même que les carrés plus petits mais avec
des tailles différentes (même si cela marche avec la même taille, mais serait
trivial). Relation { (a² + b² + c² + d²) – 2(a4 + b4 + c4 + d4) }2 = 64 a²b²c²d² |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Voir liste des
liens pour le théorème de Pythagore |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/TripQuad.htm
|
Formes linéaires