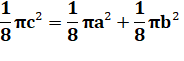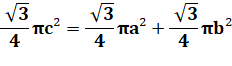|
Édition du: 06/12/2021 |
|
INDEX |
Théorème de Pythagore – Extensions |
|||
|
Pythagore en linéaire (triple quad) |
||||
![]()
|
Théorème de Pythagore valable pour toute figure On e connait le
théorème de Pythagore que sous sa forme des trois carrés accolés au triangle
rectangle. Savez-vous que la propriété est vraie pour toute forme non limitée
au carré, memê quelconque, pourvu qu'elles soient semblables. |
||
|
|
Sommaire de cette page >>>
Pythagore sous toutes les formes >>>
Démo d'Einstein >>>
Pythagore avec triangles quelconques >>> Démo avec
aires des triangles |
Débutants Glossaire |
Voir Types de démonstrations
du théorème de Pythagore / Généralisation du
théorème de Pythagore
|
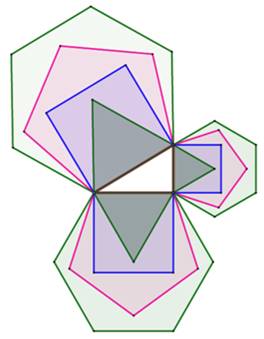
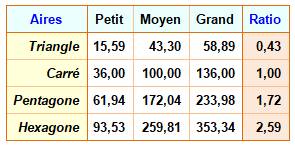
Polygones Ce dessin
montre les polygones de 3 à 6 côtés apposés aux trois côtés d'un triangle
rectangle (6; 10; 11,662). Le
tableau indique les aires mesurées. Dans les
quatre cas, la somme des aires des deux plus petits polygones est égale à
celle du plus grand. Explication Si la
propriété est vraie pour les carrés, il est normal qu'elle soit valable pour
des figures qui leur sont proportionnelle. La
colonne ratio du tableau indique le rapport de proportionnalité entre les
aires des figures. Pour le triangle, par exemple, toutes les aires indiquées
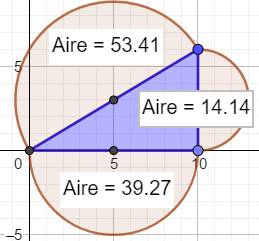
sont égales à celles des carrés multipliées par 0,433… Toute forme On
connait le cas du carré, mais cette propriété s'étend donc à tous les
polygones et à toute forme droite ou courbe. Dans le
cas du demi-cercle, on vérifie bien la relation sur les aires: 14,14 + 39,27
= 53,41. En effet,
pour le demi-cercle, le rapport de proportionnalité est égal à Pi / 8 = 0,3927…
Pour les
triangles, on aurait:
|
|
|
Voir Brève de
maths 481
|
Approche Triangle
rectangle et une des hauteurs. Duplication
du triangle initial et des deux nouveaux triangles rectangles, chacun apposé
aux côtés De manière
évidente, la somme des aires des deux triangles internes est égale à celle du
triangle complet Du fait
des égalités des triangles, on a la même propriété avec les triangles
externes: Comment prouver le théorème avec ces données? Démonstration d'Einstein Avec des
angles identiques, ces trois triangles sont semblables.
Leur aire
est proportionnelle à celle d'un triangle rectangle "unitaire":
hypoténuse = 1 et aire = X. Donc,
proportionnelle au carré de l'hypoténuse. Aire verte + aire bleue = aire
jaune c²X = a²X = b² X c² = a² + b² |
|
|
|
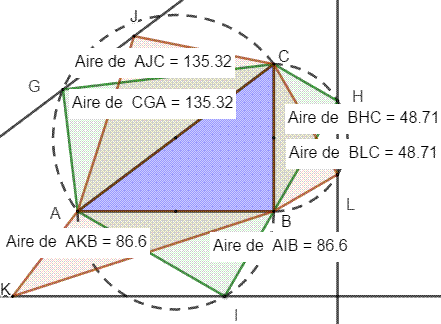
Pythagore avec des triangles quelconques Comment construire trois triangles quelconques autour d'un triangle
rectangle tout en ayant la propriété de Pythagore ? Triangle rectangle
en bleu. Demi-cercle
sur les côtés. Une
droite à angle donné partant des sommets; intersection avec le cercle et
triangle en rejoignant l'autre sommet (en vert). Inscrits
dans un demi-cercle les triangles sont rectangles; ils ont les mêmes angles;
ils sont semblables. La somme
des aires des deux petits est égale à celle du grand: 48,71 + 86,6 = 135,32. Avec des
parallèles aux côtés du triangle
initial, on peut construire autant de triangles, non rectangles (marron), de
même aire, et avec la même propriété. |
|
|
Voir Théorème de Pappus-Clairaut
avec les parallélogrammes
|
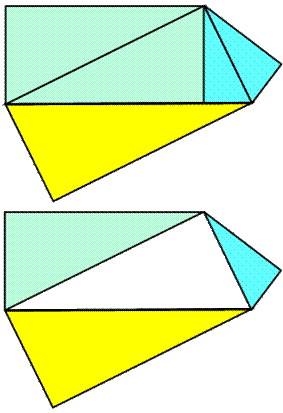
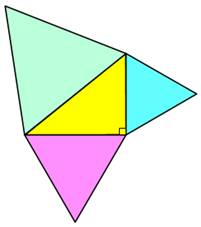
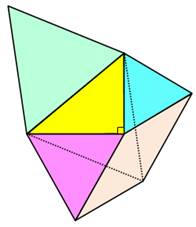
Figure de gauche en haut On utilise
ici, non pas les carrés, mes les triangles équilatéraux apposés aux côtés du
triangle rectangle. Comment
monter que la somme des aires des deux petits (bleu et mauve) est égale à
celle du grand (vert) ? Comme
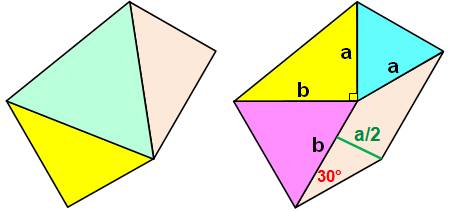
souvent, quelques constructions sont nécessaires. Figure de droite en haut Premièrement,
on replie le grand triangle sur l'hypoténuse (pointillé). Avec ce
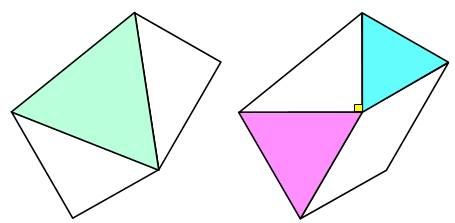
nouveau sommet, on construit le parallélogramme ocre. Figures du centre De la
figure en haut on isole le pentagone avec deux découpes:
Comparaison Les deux
triangles rectangles (jaunes) sont égaux. Un des
angles du losange vaut (90 – 60) = 30°; sa hauteur est donc égale à a/2 et
son aire vaut: 1/2 ab, identique à celle du triangle rectangle. Les deux
figures marron clairs sont
de même aire. Conclusion Les deux
figure dépouillées de surfaces égales montrent que l'aire du grand triangle
vaut la somme des deux autres. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
A Pythagorean Theorem for
Pentagons + Einstein's Proof El teorema de Pitagoras via triangles – Vidéo muette |
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/Toute.htm
|