|
Édition du: 28/03/2023 |
|
INDEX |
Types de Nombres – GRILLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
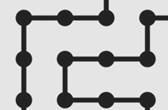
CHEMINS AUTO-ÉVITANTS (CAE)
Chemin dessiné
sur une grille (anglais: lattice path). Déplacement
horizontaux et verticaux le long des arrêtes. Interdit de
repasser par un point déjà rencontré.
|
||
|
|
Sommaire de cette page >>> Chemins auto-évitants de base >>> Chemins auto-évitants (CAE) >>> Chemins zigzags >>> Chemins ficelles >>> En bref: très complexe |
Débutants Glossaire |
|
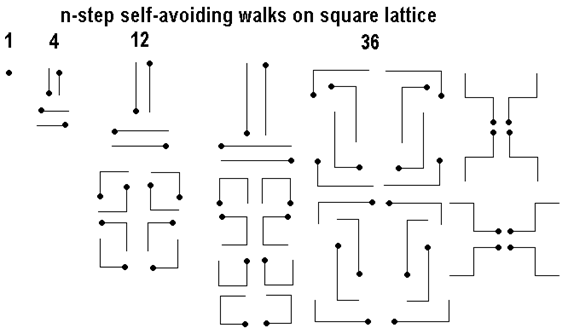
Sur réseau rectangulaire Quantité de chemins:
Liste: 1, 4, 12, 36, 100, 284, 780, 2172, 5916,
16268, 44100, 120292, 324932, 881500, 2374444, 6416596, 17245332, 46466676,
124658732, 335116620, … Le calcul de ces valeurs est souvent un test de
performance des ordinateurs, voire d'ingéniosité algorithmique. |
Quatre de longueur 1
|
||
|
Exemple avec illustration |
Source image: Bottomley |
||
|
Sur réseau carré type Manhattan Quantité de chemins selon la taille du carré pour
une des catégories (par exemple: départ avec un pas à droite). Il en existe
de nombreuses variétés. Voir Références La littérature anglaise sur le sujet est très
copieuse mais peu explicite simplement. Articles universitaires. Malgré une définition simple, les chemins
auto-évitants sont des objets mathématiques dont la compréhension fait appel
aux théories mathématiques les plus en pointe. |
Un exemple 1, 2, 4, 8, 14, 26, 48, 88, 154, 278, 500, 900, 1576, 2806, 4996,
8894, 15564, 27538, 48726, 86212, 150792, 265730, 468342, 825462, 1442866,
2535802, 4457332, 7835308, 13687192, 24008300, 42118956, 73895808, 129012260,
225966856, 395842772, 693470658, … OEIS A117633 / A006744
… |
||
|
Dénombrement sur réseau carré |
Il est possible d’énumérer tous les tracés différents
de faible longueur, mais il n’existe pas de formule explicite qui donne le
nombre de tracés en fonction de n. Il est démontré que ce nombre contient un
terme qui se comporte à l’infini comme μ à la puissance n. μ est compris entre 2 et 3, mais seules des
simulations numériques nous renseignent sur sa valeur exacte : μ est
approximativement égal à 2,638. |
||
|
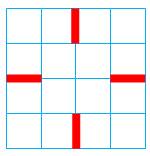
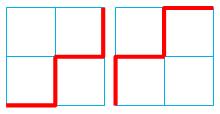
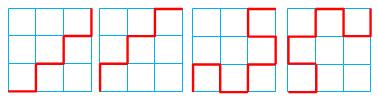
Un chemin zigzag relie de coin bas-gauche au coin
haut-droite en suivant le quadrillage d'une grille carrée. Contrainte: jamais deux pas consécutifs dans la
même direction. Combien de chemins possibles selon la taille du
carré ? Il y a 2 chemins sur le carré 1 × 1; Il y a 2 chemins sur le carré 2 × 2; Il y a 4 chemins sur le carré 3 × 3; |
|
||
|
Nombres chemin zigzag |
1, 2, 2, 4, 10, 36, 188, 1582, 20576, 388592, 10461898, 408377408,
23652253982, … OEIS A034165 & A034166 |
||
|
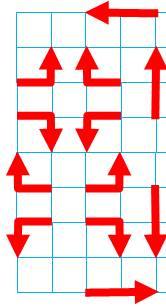
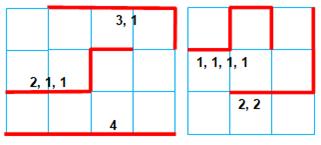
Chemin d'une ficelle de longueur fixe, posée sur
le quadrillage changeant de direction à chaque pas. Croisement autorisé, mais sans repasser sur une
arête On peut les dénombrer en utilisant les partitions
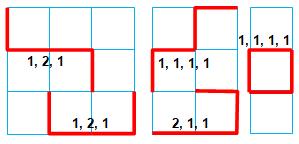
de 4:
|
|
||
|
Nombres ficelle |
1, 1, 2, 4, 10, 24, 66, 176, 493, 1362, 3821, 10660,
29864, 83329, 232702, 648182, 1804901, … OEIS
A001997 |
||
En bref: auto-évitant, monde très complexe
|
Combien de
chemins auto-évitants ? Cela dépend de
la forme du réseau et des contraintes imposées aux chemins. Sur un réseau hexagonal,
on aura par exemple: 3 chemins de longueur 1 partant d'un point donné; 6 de
longueur 2 ; 12 de longueur 3 ; 24 de longueur 4 ... 33 471 chemins pour 14. Le calcul de la
quantité de chemins est d'une complexité telle que les mathématiciens
s'attachent plutôt à chercher un ordre de grandeur de ce nombre. On sait que le
nombre de chemins de longueur n est proche, pour n grand, de la puissance
nième d'une constante µ , la constante de
connectivité du réseau. Dans le cas du
réseau hexagonal, le Français Hugo Duminil-Copin
et le Russe Stanislav Smirnov (médaille Fields
2010) ont établi que cette constante était égale à (2 + 21/2)1/2
= 1,8477…. Mais, aucune généralisation possible. Intérêt des ces
recherches: répondre aux chimistes des polymères qui furent les premiers
utilisateurs des chemins auto-évitants. Dans leur cas, les arêtes sont
remplacées par des liaisons moléculaires. Quand le polymère est plongé
dans un liquide au fort pouvoir de dissolution, il se déplie et est libre de
ses mouvements. Soumis à l’agitation thermique, il adopte alors au cours du
temps toutes les configurations possibles du chemin auto-évitant. Autre exemples: cours des rivières, frontière des pays, … tracés
fractals, transition de phase, notamment aimantation. Applications aussi
en mécanique statistique et en génie logiciel. |
D'après Partons
sur les chemins auto-évitants – Roger Mansuy – 2017
Haut de page (ou
double-clic)
![]()
|
Suite |
·
Chemin de la fourmi sur pavé, cylindre
… ·
Graphe
– Index ·
Courbes de
Peano et autre tracés fractals |
|
Voir |
·
Jeux
– Index ·
Topologie – Glossaire |
|
·
Les
chemins aléatoires – Wendelin Werner – Pour la Science – N286 – Août 2001 ·
Self-avoiding Walks –
OEIS – Une revue des différents types ·
Chemin
auto-évitant – Wikipédia ·
Self-avoiding
walk – Wolfram MathWorld ·
Chemins
auto-évitants : autour de la constante de connectivité – Cécile Gachet ·
Chemins
auto-évitants – A. Esculier –
Exemple et programmation Maple |
|
|
Cette page |