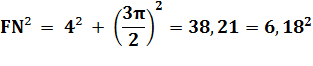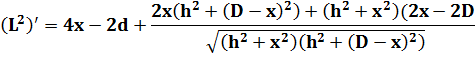|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CYLINDRE CREUX – Trajet de la Fourmi
Comment déterminer les
distances sur un cylindre? Quelle est la longueur la
plus courte d'un point à un autre? Énigme de la fourmi qui se
dirige au plus vite vers une goutte d'eau en circulant sur un récipient
creux. Problème similaire sur
cylindre plein >>> |
Voir
Fourmi sur pavé
|
|
||
|
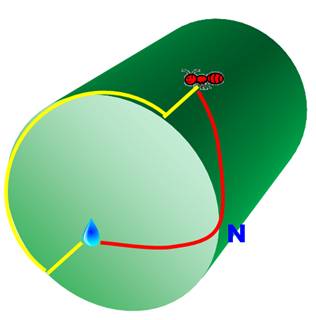
Énigme Une
fourmi se trouve sur l'extérieur d'un cylindre creux
(comme une boite de conserve ouverte ou un bocal de confiture). Elle
avise une goutte d'eau qui se trouve de l'autre côté mais à l'intérieur. Plus précisément en un point
diamétralement opposée à sa position. Quel est
le chemin le plus court pour atteindre la goutte d'eau? Approche La fourmi
peut monter tout droit pour atteindre le bord, faire le tour sur le bord (un
demi-périmètre) et descendre droit sur la goutte d'eau (trajectoire jaune).
Sans doute pas le plus court chemin! Nous
avons l'intuition que: monter en biais atteindre le bord en N puis descendre
en biais devrait faire gagner du chemin. Comment
le justifier et calculer les longueurs des chemins en jaune et en rouge. |
Illustration
Exemple numérique: chemin en jaune Cylindre de rayon: 3 cm; périmètre: 6 Distance fourmi-bord en ligne droite: 4 cm Distance goutte-bord en ligne droite: 4 cm Ljaune = 4 + 3 Lrouge = ? Comment le calculer ? |
|
|
|
||
|
Méthode de résolution de problèmes
de trajectoires sur un cylindre Une
astuce pratique (géométrique) va permettre une résolution facile sans
s'embarquer dans des calculs compliqués. La solution analytique fait intervenir la dérivée d'une fonction du
deuxième degré associée à une racine carrée couvrant une fonction du
quatrième degré. Imaginez
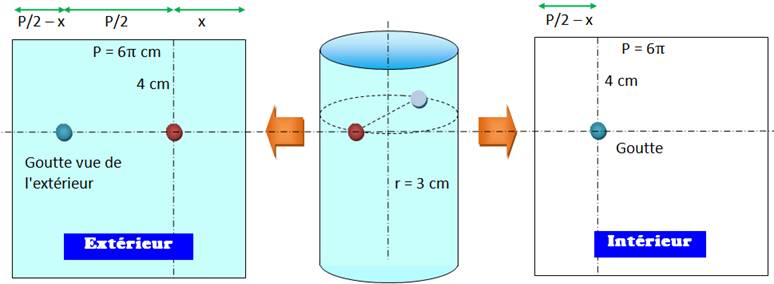
que nous ayons collé une feuille de papier sur l'extérieur du cylindre et que
nous avons fait la même chose sur la face intérieure. Nous coupons le
cylindre le long d'une verticale et nous nous
retrouvons avec deux feuilles en forme de rectangle. Notons la
position de la fourmi à une distance x du bord de coupe; vue de l'extérieur, la
goutte se trouve un demi-tour plus loin, soit un demi-périmètre; alors, la
distance de la goutte à l'autre bord de coupe est égal à P + P/2 – x = P/2 –
x.
Comment y
représenter le parcours de la fourmi? Un trait
sur le rectangle extérieur qui joint la fourmi au bord du cylindre, disons un
point M. Et un trait sur le rectangle intérieur qui part de M pour rejoindre
la goutte d'eau. Choisissons
le point M au sommet de notre verticale de coupe: coin supérieur droit du
rectangle extérieur ou coin supérieur gauche du rectangle intérieur. C'est le
point de passage du "sommet" pour la fourmi. Rejoignons les
feuilles le long de la verticale de coupe. On note bien que la fourmi devra
obligatoirement passer par le point "sommet" M pour passer du monde
extérieur au monde intérieur. |
||
|
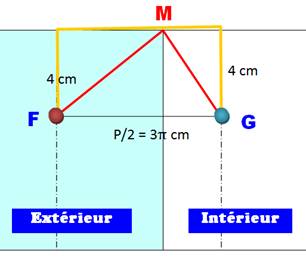
Nous
retrouvons le trajet jaune et le trajet rouge représentés sur ces surfaces
développées. Tous les deux passent par F, M et G. Il est
maintenant évident que le rouge est plus court. Reste à trouver quel est le
plus court parmi tous les trajets rouges possibles. Notre
intuition nous dit que ce sera le cas si M est au milieu, sur la médiatrice
de FG. |
|
|
|
|
||
|
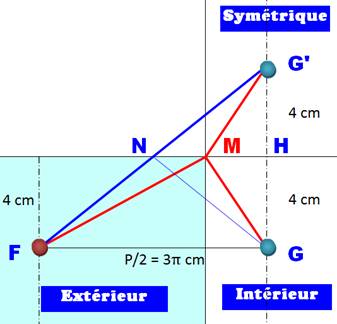
Pour
trouver le trajet le plus court, nous allons dessiner le symétrique du
rectangle représentant l'intérieur du cylindre. G' est
symétrique de G: HG = HG' HM est la
médiatrice de GG': MG' = MG. Les chemins FMG et FMG'
sont de même longueur. Par la
relation d'inégalités des triangles: FM + MG' Le chemin
le plus court, est donc atteint lorsque M est situé sur FG' avec FM + MG'
= FG' Or M et N
sont à la fois sur FG' et sur la médiatrice de GG'. Les
points M et N sont confondus. |
Cette figure montre que le trajet minimal de la
fourmi est le segment FNG' ou en retournant le dernier tronçon: FNG, avec FN
= NG. Application numérique
à comparer à 17,42
cm en suivant le bord. |
|
Note: Cette
démonstration géométrique est utilisée en optique: trajets réfléchis par les
miroirs
|
|
||
|
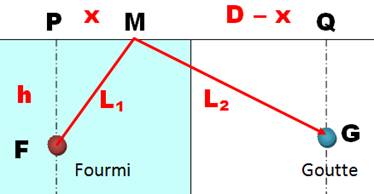
Plaçons
le point M n'importe où sur le bord. Le trajet
le plus court est en ligne droite, propriété bien connue. Reste à
calculer la distance L et à chercher son minimum. Toutes
les valeurs concernées sont des longueurs donc des grandeurs positives. Nous
pouvons travailler sur les carrés.
|
La longueur L = L1 + L2 est
minimale pour M au milieu de PQ |
|
|
En
explicitant!:
Les
calculs donnent bien la réponse, mais c'est très laborieux. Sans
expliciter les calculs (compliqués), la dérivée de L² est:
Qui est
nulle pour: x = D / 2 |
||
|
Le
calcul du trajet le plus sur un cylindre creux ne présente pas de grande
difficulté. Le développement du cercle sur un plan permet de résoudre ce
problème. Faire bien attention au point de passage du trajet de l'extérieur à
l'intérieur. La méthode du miroir
(des symétries)
permet de résoudre la figure. |
![]()
|
Suite |
|
|
Aussi |
|
|
Cette page |
![]()