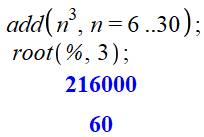|
Édition du: 05/11/2024 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
|
Système sexagésimal 10010 = [1, 40]60
100010 = [16, 40]60
10 00010 = [2, 46, 40]60
|
|||
|
Caractérisation
du nombre
|
|
Voir |
||
|
Sexagénaire:
si les années étaient des secondes,
aujourd'hui j'aurais vécu une minute.
Georg Christoph Lichtenberg Passé soixante ans, quand on se réveille sans avoir
mal quelque part, c'est qu'on est mort.
Ricet Barrier Ce qui me console de
souffler bientôt ma soixantième bougie,
c'est que dans sexagénaire il y a sexe. Guy Bedos Quel âge avez-vous?
J'ai 60, cette année. Ah! 67
années, vous êtes à la retraite, alors! À cet âge, sois sans temps et réjouis-toi du temps qui
passe. Le Pont-NEUF fait un soixante PIEDS - Contrepèterie |
Voir
Pensées & humour
Amusement d'enfants avec 60

Chiffres et numération
|
60 =
669 = 5511 = 4414 =
3319 = 2229 = 1159 |
|
|
60 =
6+0 + 3+6 + 32+62 |
Somme de ses chiffres, de ceux de son carré
et de leur carré. |
|
N60 |
On compte encore aujourd'hui le temps et les angles
en base 60. |
|
60
+ 6 = 66 = T11 |
|
|
60
= 11 + 13 + 17 + 19 |
|
|
Les plus anciennes traces des nombres premiers ont été trouvées au
Congo en 1950. On y trouve ces nombres premiers : Vrai ou interprétation modernes de
nos savants ? La question reste ouverte.
Voir Nombres
premiers – Historique |
|
Addition – Partitions
|
60
= 4 + 5 + … + 10 + 11
= 10 + 11 + 12 + 13 + 14
= 19 + 20 + 21 |
|
|
60
= 5 + 55 |
|
|
60
= 5 + 7 + 9 + 11
+ 13 + 15 = 8 + 10 + 12 + 14 + 16 = 10 + 11 + 12 + 13 + 14 = 15 x 4 = 4
+ 5 + … + 11 = 12 x 5 = 3 x 20 |
|
|
60
= 11 + 13 + 17 + 19
= 29 + 31 |
|
|
60
=
(15 + 1) + (15 – 1) + (15 x 1) + (15 / 1) |
|
|
60 = 29 + 31 60 = 23 + 37 60 = 19 + 41 60 = 17 + 43 60 = 13 + 47 60 = 7 + 53 |
|
|
60
= 1 + 3 + 4 + 5 + 12 + 15
+ 20 |
|
|
1 + 2 + 3 + 4 + 5 + 6 + 10 + 12 + 15 + 20 + 30 = 108 |
|
![]()
Multiplication
|
60
= 5 x 12 |
|
|
60 = 3 x 4 x 5 60 =
(1! x 2!) (3! + 4!) |
|
|
|
|
|
2 x
30 = 60 3 x
20 = 60 4 x
15 = 60 5 x
12 = 60 6 x
10 = 60 |
|
|
60 |
|
Division – Diviseurs
|
60
possède 12
diviseurs |
|
|
60
= PPCM (1, 2, 3, 4, 5, 6) = 2 x 3 x 2 x 5 |
|
|
1, 2, 3, 4, 5, 6 |
|
|
60
=> {7, 11, …59} |
|
|
60 = 10 + 20 + 30 = … =
1 + 2 + 4 + 5 + 6 + 10 + 12 + 20 |
|
|
60, 70, 84, 105, 140, 210, 420 |
|
|
12 diviseurs
|
|
|
60 est divisible par 1, 2, 3, 4, 5, 6 et pas par
7 et 8 |
|
|
60
divise
le triplet |
|
|
60
= |
|
|
|
La fonction
oméga compte les facteurs uniques et oméga majuscule, les facteurs
répétés. |
![]()
Avec les puissances
|
60
= 16² – 14² =
8² – 2² |
|
|
60
= 26 – 22 = 43 – 41 |
|
|
60 =
1² + 1² + 3² + 7² = 1² + 3² + 5² + 5² = 2² + 2² + 4² + 6² |
|
|
60 = 23 + 33
+ 52 = 25 + 31 + 52 |
|
|
55² + 56² + … + 59² + 60² =
61² + 62² + … + 65² = 19 855 |
|
En puissance
|
603 = 63 + 73 + … + 303
= 216 000
|
Exemple de
formulation du calcul: addition des cubes de n de n = 6 à n = 30; puis,
racine cubique (root (%, 3) de ce résultat (%). |
Jeux et curiosités
|
60 =
20 + 20 + 20 60 =
55 + 5 |
|
||||||||||||||
|
60
= 4 x 4 x 4 – 4 = 44 + 4 x 4 |
|
||||||||||||||
|
|
|
||||||||||||||
|
60
/ (6 + 0) = 10 |
|
||||||||||||||
|
|
Autour du nombre
|
|
|
![]()
Géométrie
|
60
°
|
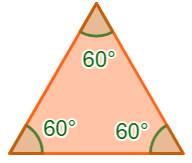
Problème Soit un cube, relions un sommet à deux
sommets opposés. Que vaut l'angle ainsi formé? Solution Le triangle est formé de trois diagonales
de face du cube; Elles sont égales. Le triangle est
équilatéral; L'angle vaut 60 degrés. |
|
10 13 13 8 15 17 13 13 24 6 25 29 |
|
Suite
en Géométrie / Géométrie – Index
|
Question Pensez
à un nombre n inférieur à 60 et donnez-moi simplement le reste de la division
par 3, par 4 et par 5, disons a, b et c. Je devine le nombre Je
calcule secrètement: S = 40a + 45b + 36c Le
nombre n est égal au reste de la division de S par P = 60 = 3x4x5. Exemple: Si n = 57,
alors: a = 0, b = 1 et c = 2. S
= 45 + 72 = 117 = 1 x 60 + 57 Calcul des coefficients 60
= 3 x 4 x 5 le produit des trois diviseurs 40
est le plus petit multiple de 4 x 5 tel que, diminué de 1, il est divisible
par 3. 45
est le plus petit multiple de 3 x 5 tel que, diminué de 1, il est divisible
par 4. 36
est le plus petit multiple de 3 x 4 tel que, diminué de 1, il est divisible
par 5. Avec quatre nombres P
= 3 x 4 x 5 x 7 = 420, alors: S = 280a + 105b+ 336c + 120d D'après
Bachet
de Méziriac - Problèmes plaisans et délectables |
Voir Magie / Résolution
générale (Restes chinois)
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
60 2,
[1, 1, 1, 1, 0, 0] 3,
[2, 0, 2, 0] 4,
[3, 3, 0] 5,
[2, 2, 0] 6,
[1, 4, 0] 7,
[1, 1, 4] 8,
[7, 4] 9,
[6, 6] 10,
[6, 0] 11,
[5, 5] |
12,
[5, 0] 13,
[4, 8] 14,
[4, 4] 15,
[4, 0] 16,
[3, 12] 17,
[3, 9] 18,
[3, 6] 19, [3, 3] 20,
[3, 0] 21,
[2, 18] |
22,
[2, 16] 23,
[2, 14] 24,
[2, 12] 25,
[2, 10] 26,
[2, 8] 27,
[2, 6] 28,
[2, 4] 29,
[2, 2] 30,
[2, 0] 60,
[1, 0] |
9, [6, 6] 11,
[5, 5] 14,
[4, 4] 19,
[3, 3] 29,
[2, 2] 59,
[1, 1] |
Voir Bases / Brésiliens
![]()
|
Suite |
|
|
Cette page |
![]()