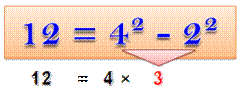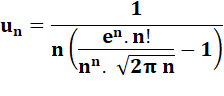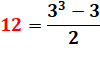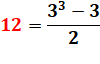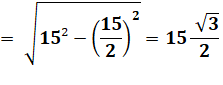|
Édition du: 29/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Nombre 12 |
|||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
Préfixes
diviseurs et multiplicateurs: 10-12 pico 10 12 téra (billion) Notez 109 en Fr =
milliard; É-U= billion |
||||
|
Caractérisation
du nombre
|
Voir Nom des nombres |
Voir |
||
Rappel
Propriétés générales >>>
|
Candice
& De Fondouze |
|
Mon premier est un féculent; Mon second est un féculent; Mon troisième se trouve dans la salle de bain; Mon tout est la base mathématique portugaise... |
|
Les huitres en conversation: - Qu'en pensez-vous ? Pour bien
faire au réveillon, il faudrait qu'on soit une douzaine,
non ? |
Voir Pensées
& humour / Prénoms
Numération
– Chiffres – Type de nombre
|
|
||
|
12 +
21 = 33 12 × 21 = 252 |
|
|
|
12 =
4 (1 + 2) = 6 (1 x 2) |
|
|
|
12
|
|
|
|
12
= 1 + 2 + 1² + 2² 12
= 1 + 2 + 1 + 4 + 4 |
Somme de ses chiffres et des carrés de ses
chiffres. Somme de ses chiffres et de ceux de son
carré. |
|
|
12,
24, 36, 48 21,
42, 63, 84 |
Les
nombres du premier sont les seuls à être quatre fois la
somme de leurs chiffres; ceux du second les seuls à l'être sont sept
fois. |
|
|
12:
{26, 34, 43, 62, 223, 232, 322} |
|
|
|
12
= ½ (3 x 3² – 3) |
|
|
|
1 – 2 + 3 + 4 + 6
= 12 |
|
|
|
12
x 9 = 108
et 1 + 0 + 8 = 9 89
x 9 = 801 |
|
|
|
12 = 2 (2 x 3) = 4 T2 = CC2 –
1 = 2² + 3²
– 1 5² + 12² = 13² 10² + 11²
+ 12² = 13² + 14² |
Ensemble,
ces propriétés sont communes à toute une série de nombres: 4, 12, 24, 40 … |
|
|
1210 = 1111 = 225 |
|
|
|
12 = 4 x (1 +
2) & 21 = 7 x (2 + 1) 24 = 4 x (2 + 4) & 42 = 7 x (4 +
2) 36 = 4 x (3 + 6) & 63 = 7 x (6 +
3) 48 = 4 x (4 + 8) & 84 = 7 x (8 +
4) |
|
|
|
12 =
2 x 6 |
|
|
|
12
= 8 + 3 + 1 = 10101Binaire-Fibonacci |
Somme de
nombres de Fibonacci distincts et non consécutifs. Cette représentation est
unique pour tout nombre. |
|
Addition
– Partition
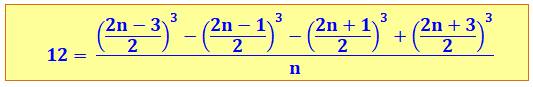
Identité
impliquant quatre nombres impairs successifs
Voir Brève 61-1218
|
P(12) = 77 |
|
|
12 =
5 + 7 |
|
|
12
= 1 + 4 + 7 |
|
|
12
= 3 + 4 + 5 21 = 6 + 7 + 8 |
|
|
12 =
1 + 5
+ 6 = 2 + 3
+ 7 62
= 1² + 5² + 6² = 2² + 3² + 7² |
|
|
Multiples
de 12 4² – 2² = 12 5² – 1² = 24 6² – 0² = 36 |
1000 = 4 x 250 = 251² – 249²
|
|
12 =
5 + 4 + 3 = 2 x 6 |
|
|
12
= 3 + 4 + 5 = 6 x 2 |
|
|
12 = 1+1+1+1+2+6 = 1+1+1+1+1+3+4 =
1x1x1x1x2x6 = 1x1x1x1x1x3x4 |
|
|
|
|
|
12 entiers consécutifs |
|
|
12 =
(3+1) + (3–1) + (3x1) + (3/1) |
|
|
|
|
![]()
Multiplication
– Division
Table
de multiplication du 12

Voir
Table
complète
|
12 / (1 + 2) = 4 |
|
||
|
12
= 3 x 4 56 = 7 x 8 |
|
||
|
12 divisible
par 3 et 2 |
|
||
|
12 = 22 ∙ 3 = 13 ∙ 22 ∙ 31 |
|
||
|
12 = 2² x 3 13 = 13 |
|
||
|
12 = 2 x 6
= 3 x 4 |
|
||
|
12 =
1! x 2! x 3! 12 =
4! / 2! |
|
||
|
12 =
SP(4) = PPCM(1, 2, 3, 4) |
|
||
|
12
= (5 – 1) (5 – 2)
= 4 x 3 |
|
||
|
3 x 4 = 12 33 x 34 =
1122 333 x 334
= 111222 etc. |
|||
|
12 = PPCM (1, 2, 3, 4)
= 2 x 3 x 2 |
|
||
|
12 x 5 10n
= 6 10n+1 |
|
||
|
abc x 12 = uvwt 5abc x 12 = 6uvwt |
Vrai jusqu'à abc = 833. >>> |
||
|
3456
/ 12 = 288 |
|
||
|
12 |
|
||
|
12
|
5
+ 7 = 12 11 + 13 = 24 |
|
12
si n est impair |
2 x 3 x 4 = (3 – 1) 3 (3 + 1) = 24 4 x 5 x 6 = (5 – 1) 5 (5 + 1) = 120 |
|
1 / 12,25125 = 0,08 16 24 … |
|
![]()
|
|
|||
|
1 + 2 + 3 + 4 + 6 = 16 & 16 > 12 |
|
||
|
|
|
||
|
1 + 3 + 4 +
6 =
2 + 12 = 14 = 28 / 2 |
|
||
|
10 / 12 =
0,8333… 20 / 12 =
1,666… 30 / 12 =
2,5 40 / 12 =
3,33… 50 / 12 =
4,1666… 60 / 12 = 5 |
70 / 12 = 5,8333… 80 / 12 = 6,66… 90 / 12 = 7,5 100 / 12 = 8,333… 110 / 12 = 9,1666… 120 / 12 = 10 |
|
|
|
12 divise (d-a)(c-a)(b-a) … |
|
||
|
12, 12 12 12 12 … = 400 / 33 = 2 / 0,165 |
|
||
|
|
|
||
|
|
Tau est la quantité de
diviseurs; Sigma: la somme. Seul autre nombres
sublimeconnu: |
||
|
12
= |
|
||
|
|
|
||
|
12, 24, 48, 72, 144, 240, 432, 480, 576, 720,
1152, 1440 … |
|
||
|
|
|
||
|
12 Ses
facteurs premiers: ( 2 , 3) Produit:
2 x 3 x 12 = 72 Quantité
de diviseurs de 72: 12 |
|
||
|
12 => {5, 7, 11} |
|
||
|
PGCD(12,
2k+1 < 12) = 1 |
|
||
|
|
Autres
avec les diviseurs de 120, 720, 2520, 10 080, 30 240, 75 600, 604 800 Davenport
en 1952 cité par Le Lionnais |
||
Puissances
|
12 =
10 + 21 + 32 |
|
||
|
12 =
1 + 2 + 13 + 23 |
|
||
|
10²
+ 11² + 12² = 13² + 14² = 365 |
|
||
|
|
|
||
|
12 =
2² + 2² + 2² = 1² + ² + 1² + 3² = 13 + 13 + 13
+ 13 + 23 |
|
||
|
12
= 4² – 2² = 6 x 2 |
|
||
|
12
= 472 – 133 = 2 209 – 2 197 |
|
||
|
= 0,115629056…
+ 11,884370943542… |
|||
|
12 = 31 + 32
= 24 – 22
= 42 – 41 |
|
||
|
= 343 + 1000 - 1331 |
|
||
|
13
– 2x23
+ 33 = 6 x 2 |
|
||
|
12
= 175 – 165 – 135 |
|
||
![]()
Nombre
en puissances
|
38² = 1444 2 538² = 6441444 |
|
|||||||
|
12²
= 144 102² = 10404 120² = 144000 21² = 441 120² = 14400 210² = 441000 (1 + 2)² = 1 + 4 + 4 = 9 |
Voir Nombre 1137 |
|||||||
|
12²
= 1 x 2 x 3 x 4 x 6 = 144 |
|
|||||||
|
122 – 1 =
143 123 – 1 =
1727 = 11 x 157 |
|
|||||||
|
12² +
33² = 1 233 88²
+ 33² = 8 823 |
|
|||||||
|
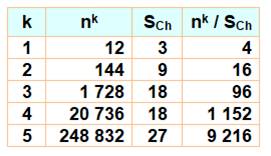
125 = 45 + 55 + 65
+ 75 + 95 + 115 = 248 832 |
|
|||||||
|
12n |
|
|||||||
|
|
|||||||
![]()
Autour
du nombre
|
|
|
|
11 x 1,1 = 12,1 Autre solution ( entière) 2
+ 2 = 4 2
x 2 = 4 |
X² – X.S + P = 0 Y = S – X |
|
F12 = 144 = 122 12 = 1 + 1 + 2 + 3 + 5 |
|
|
12! =
210 x 467775 = 210 x 35 x 52 x 7 x
11 = 479001600 |
|
|
12! – 1 = 479 001 599 |
|
|
|
n= 10 => 11,95405959
100 => 11,99505324
1000 => 11,99961601 10000 => 12,00192031 20000 => 11,99904008 |
Jeux – Amusements – Dénombrements

|
12 et
21 24
et 42 |
|
|
|
12 x
0495 = 5 940 012 x
210 = 120 x 021 = 2520 |
|
|
|
12 x 9 + 3 = 111 123 x 9 + 4 = 1111 1234 x 9 + 5 =
11111 |
|
|
|
1225 = 35² 112225 = 335² 11122225 = 3335² … |
|
|
|
12 x
483 = 5 796 42
x 138 = 5 796 |
|
|
|
12
divise
le triplet |
|
|
|
5, 5, 6 => 12 5, 5, 8 => 12 |
|
|
|
Triangle isocèle base = 30 côtés = 25 Côté carré inscrit = 12 |
|
|
|
|
|
|
|
|
|
|
|
|
7, 8, 9, 77, 78, 79, 87, 88, 89, 97, 98, 99. |
|
Faire 12
avec quatre fois chacun des chiffres
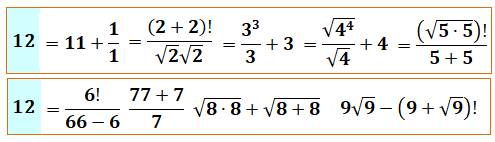
|
|
|
|
12 = ( 0! + 0! + 0!
)! x
( 0! + 0! ) |
|
|
|
|
|
– 1/12 = 1 + 2 + 3 + … (?) |
|
|
|
|
|
|
|
|
12,4 kg = 400 onces troy |
|
|
12,56 = 4 = 12,566 370 61 |
Stéradian Angle solide d'un cône dans une
sphère de rayon unité, ayant le même centre et embrassant une surface de 1 |
|
12,99038106…
|
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 1, 0, 0] 3,
[1, 1, 0] 4,
[3, 0] 5, [2, 2] |
6,
[2, 0] 7,
[1, 5] 8,
[1, 4] 9,
[1, 3] |
10,
[1, 2] 11, [1, 1] 12,
[1, 0] |
5,
[2, 2] 11,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Site |
|
|
Cette
page |
![]()