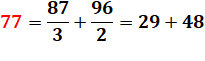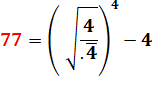|
Édition du: 05/11/2024 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
|
|
||
|
Caractérisation
du nombre
|
|
Voir |
|
Devinette – Niveau école primaire
|
|
|
|
||||
|
SEINE
ET MARNE |
||||
|
77 = 7 x 11 |
IRIDIUM
Ir |
|||
|
Propriétés Typiques |
77 = 4x4 + 5x5 + 6x6 pour arriver à 7 7 |
CACA |
||
|
|
|
|||
|
|
||||||
|
|
Voir Numération 70 à 79 |
|||||
|
Plus
petit nombre en anglais nécessitant cinq syllabes. |
||
|
le
magazine des jeunes de 7 à 77 ans. |
||
|
|
||
|
|
Chiffres et numération
|
77 + (7 + 7) = 91 = T13 77 – (7 × 7) = 28 = T7 77 × (7 × 7) = 3 773 |
|
|
|
77 = 7 x 11 |
|
|
|
77 = 7 x 11 9 797 = 97 x 101 |
|
|
|
77 = 7 x 11
7x7 = 49 => 4x9 = 36
=>3x6 = 18 =>1x8 = 8 |
|
|
|
12345678911223344556677 |
|
|
|
7x7
= 49; 4x9 = 36; 3x6 = 18; 1x8 = 8 |
|
|
Addition et soustraction
|
77 = 2 + 3 + … + 11 + 12 77 = 8 + 9 + … + 13 + 14 77 = 38 + 39 |
|
|
77 = 14 + 13 +…+ 8 = 7 x 11 |
|
|
77 = 2 + 3 + 5 + 7 +
11
+ 13 + 17 + 19 |
Voir Table |
|
77 = 70 + 07 = 16
+ 61 = 25 + 52 = 34 + 43 |
|
|
77 = P12 |
|
|
|
|
|
|
|
|
77 |
|
Multiplication, division, diviseurs
|
77 = 7 x 11 |
|
||
|
|
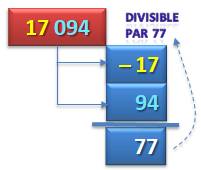
Constituer
des blocs de 3 chiffres. les
additionner et soustraire alternativement. Le
résultat doit être divisible par 77 |
|
|
|
77 = 11! / 6! ² = 11! / 720²
= 39 916 800 / 518 400 |
|
||
|
1001 = 77 x
13 |
|
||
|
1, 7, 11, 13, 77, 91, 143, 1001 |
|
|
|
|
77
x 6 77 – 1 est premier 77
x 10 77 – 1 est premier |
|
|
|
|
77 = 2² + 3² + 8²
= 4² + 5² + 6² |
|
|
77 = 4² + 5² + 6²
= 4x4 + 5x5 + 6x6 |
|
|
77 = 39² – 38² = 39 +
38
= 9² – 2² |
|
En puissance
|
|
|
|
77²
= 5 929 |
|
|
772
= 5929 = (8 + 9 + …+ 14)2 = (38 + 39)2 = 182 + 192
+ … + 282 |
|
|
773
= 456 533 |
|
Autour du nombre
|
77!
+ 1 |
(Voir 73) |
|
|
|
|
77 |
10 77+1 – 1 |
|
Jeux et curiosités
|
77 = 13 + 8x8 717 = 13 + 8x88 7117 = 13 + 8x888 … |
|
|
|
Avec
.4 surligné = 0, 444… = 4/9 |
|
7
x 7 = 49 / 4 x 9 = 36 / 3 x 6 = 18 / 1 x 8 = 8 Record
avec itération en quatre étapes ou cycles. Ce
procédé s'appelle la persistance
multiplicative. Avec
trois cycles: 39, 47, 49, 57, 66, 68, 74, 75, 79, 86, 88, 89, 93, 94, 97, 98. Plus
petit nombre avec cinq cycles: 679. |
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 0, 1, 1, 0, 1] 3,
[2, 2, 1, 2] 4,
[1, 0, 3, 1] 5,
[3, 0, 2] 6,
[2, 0, 5] 7,
[1, 4, 0] 8,
[1, 1, 5] 9,
[8, 5] 10, [7, 7] 11,
[7, 0] |
12,
[6, 5] 13,
[5, 12] 14,
[5, 7] 15,
[5, 2] 16,
[4, 13] 17,
[4, 9] 18,
[4, 5] 19,
[4, 1] 20,
[3, 17] 21,
[3, 14] |
22,
[3, 11] 23,
[3, 8] 24,
[3, 5] 25,
[3, 2] 26,
[2, 25] 27,
[2, 23] 28,
[2, 21] 29,
[2, 19] 30,
[2, 17] 60,
[1, 17] |
10,
[7, 7] 76,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Cette page |
![]()