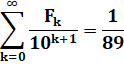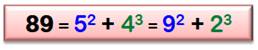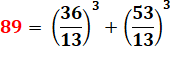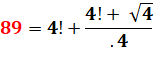NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Général	DicoNombre NOMBRES				Glossaire Général
88 87 / 86 / 85 80 70 60 50 40 30 20 10	89				90 91 92 / 93 / 94 95 100 500 1000 1 million
Nombre 89		Maths	Culture	Numération 80 à 89

CARTE D'IDENTITÉ
Nombre	Premier	Département	YONNE
Facteurs	89 = 1 x 89	Élément	ACTINIUM Ac
Propriétés Typiques	89 = 8^1 + 9²	Mnémo	FIP (France Inter Paris)
	Suite Maths		Suite Culture

Propriétés CULTURELLES

· Quatre-vingt-neuf

· Quatre-vingt-neuvième

Voir Orthographe des nombres

Espagnol Italien	Anglais Allemand
ochenta y nueve ottantanove	eighty-nine neunundachtzig

Voir Numération 80 à 89

Nombres et langues

Jeux	· 89 possibilités de monter un escalier de 10 marches avec des pas d'une, ou deux marches.	>>>
Astronomie	· 89°11' = 89,18° Déclinaison de l'étoile polaire.	Étoile polaire

Propriétés MATHÉMATIQUES

Facteurs	89 = 1 x 89
Diviseurs	1, 89
Quantité	2
Somme	90
S - N	1

· Binomial

· Coster

· Curzon

· Déficient

· Docile (amenable)

· Élégant

· Fibonacci (n° 11)

· impair

· Indice de Mersenne

· Markov

· Premier

· Premier de Chen

· Premier de Pythagore

· Premier de Sophie Germain

· Premier faible

· Premier horloge

· Premier inévitable (ou minimal)

· Premier minimal

· Premier oscillant

· Premier régulier

Voir Nom des nombres / Nombres géométriques

Chiffres et numération

			· Cousins de même forme. Voir Nombres strobogrammatiques
89 + (8 × 9) = 161	· Devient palindrome en lui ajoutant le produit de ses chiffres.
89 = (8x9) + (8+9)	· Nombre égal à produit des chiffres + somme des chiffres, comme tous les nombres à deux chiffres terminés par 9.
23, 67, 89, 4567	· Nombres premiers à chiffres consécutifs.
89	· N'est repdigit dans aucune base. Il n'est pas brésilien.
89 = 8 mod 9	· Division par 9, reste 8.
89 x 9 = 801 et 8 + 0 + 1 = 9 12 x 9 = 108		· Nombre croissant le plus grand à deux chiffres. Pour tous les nombres croissants (chiffres de plus en plus grands vers la droite) multiplié par 9, la somme des chiffres est égale à 9. · Motif palindrome avec le plus petit nombre croissant (12)
89, 187, 968, 1837, 9218, 17347, 91718, 173437, 907808, 1716517, 8872688, 17735476, 85189247, 159487405, 664272356, 1317544822, 3602001953, 7193004016, 13297007933, 47267087164, 93445163438, 176881317877, 955594506548, 1801200002107, 8813200023188			· Le plus petit palindrome retard d'ordre 24. Prendre le nombre, lui ajouter son retourné. Recommencer jusqu'à obtenir un palindrome. · 89 et 98 sont les nombres à deux chiffres qui nécessitent le plus grand nombre de telles itérations.

Addition et soustraction

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89	· 11^e Fibonacci. Le 5^e Fibonacci premier. · Son inverse est égal à la somme infinie des nombres de Fibonacci divisés par une puissance de 10.
9, 21, 31, 43, 55 et 89	· Seuls nombres non sommes de un à quatre nombres pentagonaux.

Multiplication, division, diviseurs

	· Table de multiplication du nombre 89: saut d'une unité en plus ou en moins pour les unités, les dizaines et les centaines · Principe valable pour de nombreux nombres en 111… – …11 comme 109
89 est premier 91 = 7 x 13 semi premier	· Nombre premier de Chen.
89, 97	· Premier écart égal à 8 entre premiers.
89, 179, 359, 719, 1 439, 2 879 Avec Pn+1 = 2 x Pn + 1	· Séquence de six nombres premiers de Sophie Germain (la première du genre).

Deux produits de trois nombres consécutifs ayant le même jeu de facteurs

Avec le nombre 623 présent, c'est le plus grand tel motif

Avec les puissances

89 = 5² + 8² = 2² + 2² + 9² = 2² + 6² + 7² = 3² + 4² + 8² = 1² + 4² + 6² + 6²	· Nombre binomial. · Somme de puissances. · Seules sommes de carrés jusqu'à quatre termes >>>
89 = 8^1 + 9² 43 = 4^2 + 3^3 63 = 6^2 + 3^3	· Seul nombre à deux chiffres à présenter ce motif: somme des chiffres à des puissances consécutives à partir de 1. Suivant: 135 · Motifs voisins pour 43 et 63.
		· Deux fois somme d'un cube et d'un carré. Plus petit tel motif (sans 1).
89 = 2^3 + 3^3 + 3^3 + 3^3 = 1^3 + 2^3 + 2^3 + 2^3 + 4^3		· Sommes de cubes.
89 = 45² – 44² = 45 + 44		· Motif général pour tout nombre impair.
		· Somme de deux cubes rationnels.
89, 145 …		· Début d'un cycle avec des carrés.
		· Le produit de quatre nombres consécutifs plus 1 est un carré.

En puissance

89² = 39² + 80² = 1521 + 6400 = 7921	· 15^e triplet de Pythagore primitif.
89² = 8 × 9 × 10 × 11 + 1 = 7 921	· Produit de quatre nombres consécutifs plus 1 (toujours un carré)

Autour du nombre

2 × 3 × 5 × 7 ×…× 89 – 1 premier			· Primorielle – 1 première.
M10 = 2^89 – 1	· Nombre de Mersenne (trouvé en 1911).
89	· Plus petit indice de la suite 3-Gödel à être non-entier.
899091 = 99899 x 9		· Palindrome et trois nombres successifs concaténés.
1 / 89 = 0,011235955… 1000 / 998 999 = 0,001001002003005 …		· Nombre de Fibonacci inverse (le plus petit). Contient la séquence de Fibonacci avec les premiers nombres en clair (1, 1, 2, 3, 5) et les suivants enfouis du fait de leur taille. La seconde fraction produit les nombres de Fibonacci à trois chiffres jusqu'à 610
· Toutes les fractions avec 89 au dénominateur possèdent 44 décimales répétitives en deux suites permutées.

Jeux et curiosités

	· Jeu du quatre 4. Avec .4 = 0, 4 = 2/5
89, 145, 4 , 20, 4, 16, 37, 58, 89	· Boucle dans un procédé itératif >>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 1, 1, 0, 0, 1] 3, [1, 0, 0, 2, 2] 4, [1, 1, 2, 1] 5, [3, 2, 4] 6, [2, 2, 5] 7, [1, 5, 5] 8, [1, 3, 1] 9, [1, 0, 8] 10, [8, 9] = 8910 11, [8, 1]	12, [7, 5] 13, [6, 11] 14, [6, 5] 15, [5, 14] 16, [5, 9] 17, [5, 4] 18, [4, 17] 19, [4, 13] 20, [4, 9] 21, [4, 5]	22, [4, 1] 23, [3, 20] 24, [3, 17] 25, [3, 14] 26, [3, 11] 27, [3, 8] 28, [3, 5] 29, [3, 2] 30, [2, 29] 60, [1, 29]	88, [1, 1]

Voir Bases / Brésiliens

Suite	· Nombre 90 · Voir en haut de page · DicoNombre
Cette page	http://villemin.gerard.free.fr/NombDico/Nb50a100/Nb89.htm