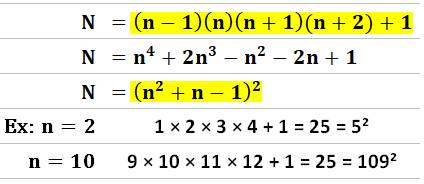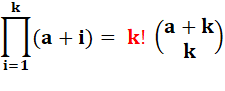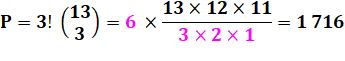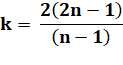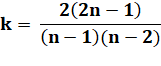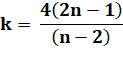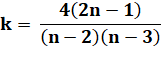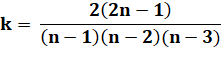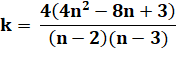|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
FACTORIELLE TRONQUÉE Factorielles généralisées Produit de p nombres
consécutifs de m à n. Elles sont utilisées en combinatoire. Soit p nombres consécutifs, leur produit est divisible
par p! Ce produit n'est
jamais une puissance. |
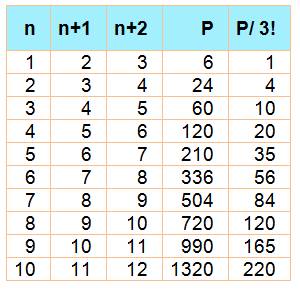
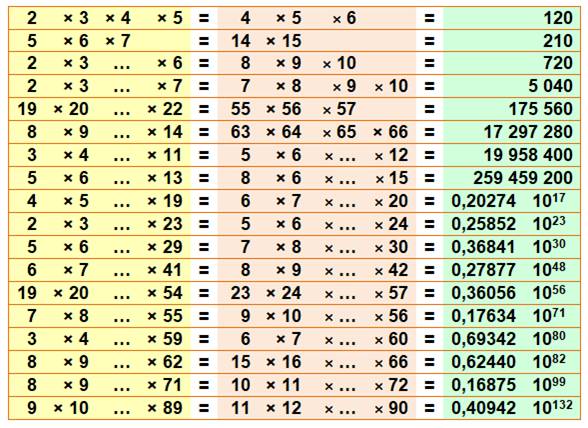
Voir Table des valeurs pour n de 1 à 10 / Brève
510
Calcul d'un produitde k nombres successifs |
|
||
|
Produit de 2 à 5 nombres
successifs: formule et exemple
Le produit de quatre
nombres consécutif plus 1 est un carré
Voir Développement |
|||
|
Calcul avec cinq nombres successifs
centrés sur 100 Le tableau montre le calcul pas à pas
conformément à la formule indiquée ci-dessus. Ce calcul est parfois présenté comme un problème
de calcul à exécuter sans calculette. |
|
||
|
Valeur pour 10, 100 et 1000 |
|
||
Voir Brève 55-1080
![]()
|
|
||
|
Théorème d'Erdös et Selfridge
(1975) Une factorielle tronquée n'est jamais une
puissance parfaite. |
n (n + 1) (n + 2) … (n + k – 1) = xL n > 0;
k, x, L > 1 n'a pas de
solution. |
|
|
Produit de nombres consécutifs
|
Exemple de calcul P = 11 x 12 x 13 = 1 716
|
|
|
Notez que l'exemple vaut
presque démonstration et |
||
Voir Calcul des combinaisons
/ Coefficients du binôme en
puissance
|
|
|||
|
Théorème d'Erdös et Selfridge Le produit de k nombres consécutifs n'est jamais
une puissance. Exemple: le produit de
trois nombres consécutifs n'est jamais un carré ou un cube. |
Rappel Le produit de
k nombres consécutifs est divisible par k!. |
||
|
Démonstration pour k = 3 On
suppose que le produit est une puissance parfaite. |
(n – 1) n (n + 1) = ak |
||
|
Deux
nombres consécutifs sont premiers entre eux. |
PGCD ((n – 1), n)
= 1 PGCD ((n + 1), n) = 1 |
||
|
C'est
donc que n est une puissance parfaite et que le produit des deux autres l'est
aussi et de la même forme. |
n = bk (n – 1) (n + 1) = n² – 1 = ck |
||
|
|
|||
|
En
rapprochant ces données: |
n = bk n² – 1 = ck (bk)² = ck + 1 |
||
|
Nous
aurions donc deux puissances consécutives, ce qui n'existe pas (sauf pour 0
et 1). |
Par contradiction, l'hypothèse initiale est
fausse et le produit de trois nombres consécutifs n'est jamais une puissance. |
||
![]()
Noms des produits de k nombres successifs
|
k |
Produit |
Facteur |
Noms |
|
2 |
n
(n + 1) |
x 1 |
= Nombre pronique |
|
|
|
x 1/2 |
= Nombre triangulaire |
|
3 |
n
(n + 1) (n+ 2) |
x 1/6 |
= Nombre tétraédrique |
|
4 |
n
(n + 1) (n + 2) (n + 3) |
x 1/24 |
= Nombre pentatope |
|
Exemple 5 ×
6 ×
7 ×
8 = 8! / 4! = 1680 Définition Nombres de
la forme 2n! / n! Notée:
n!!!! Propriété n!!!! = n ٠ (n – 1) !!!! |
Liste 1, 1, 2,
3, 4, 5, 12, 21, 32, 45, 120, 231, 384, 585, 1680, 3465, 6144, 9945, 30240,
65835, 122880, 208845, 665280, 1514205, 2949120, 5221125, 17297280, 40883535,
… OEIS A007662 |
|
Produit
de quatre nombres consécutifs + 1 = carré |
|
|
|
Montrez
que: |
n (n + 1) (n + 2) (n + 3) + 1 = c² |
|
|
Premiers
cas en exemples: |
1 × 2 × 3 × 4 + 1 = 24 + 1 = 25 = 5² 2 × 3 × 4 × 5 + 1 = 120 + 1 = 121 = 11² 3 × 4 × 5 × 6 + 1 = 360 + 1 = 361 = 19² |
|
|
Développement: |
n (n + 1) (n + 2) (n + 3) + 1 = (n² + 3n) (n² + 3n + 2) + 1 |
|
|
Posons: |
m = n² + 3n + 1 |
|
|
Notre
développement devient: |
(n² + 3n) (n² + 3n + 2) + 1 = (m – 1) (m + 1) + 1 = m² – 1 + 1 = m² |
|
|
Formulation
complète: |
n (n + 1) (n + 2) (n + 3) +
1 = (n² + 3n + 1)2 |
|
|
Autre
formule |
(n – 1) (n) (n + 1) (n + 2)
+ 1 = (n² + n – 1)² = (n (n + 1)
– 1)² |
|
|
Exemple: |
4 × 5 × 6 × 7 + 1 = (4² + 3×4 +
1)² = 29² = 841 |
|
|
Rac(9x10x11x12+1) = ? Avec la 2e formule |
On trouve ce défi sur Internet: Calculer cette racine carrée, sans calculette
|
|
|
Liste :
produit +1 = n (n + 1) – 1 |
5, 11, 19, 29,
41, 55, 71, 89, 109, 131, 155, 181, 209, 239, 271, 305, 341,
379, 419, 461, 505, 551, 599, 649, 701, 755, 811, 869, 929, 991, 1055, 1121,
1189, 1259, 1331, 1405, 1481, 1559, 1639, 1721, 1805, 1891, 1979, 2069, 2161,
2255, 2351, 2449, 2549, … |
|
Voir Identité avec quatre nombres consécutifs
|
Question Dire quand (n – 2)! +
(n + 2)! est un carré, avec n > 2. Solution En développant: (n –
2)! + (n – 2)! (n-1)(n)(n+1)(n+2) Propriété vue
ci-dessus: (n – 2)! (1 + c²) Qui est un carré si (n
– 2)! l'est. Possible que pour n = 3. (une factorielle n'est jamais un carré). Seule solution: (3 –
2)! + (3 + 2)! = 1 + 120 = 121 = 11² |
Voir DicoNombre 11
|
|
||
|
Théorème Exemple
|
||
|
|
(n+1)(n+2)…(n+p) |
|
|
|
= n! (n+1)(n+2)…(n+p) / n! |
|
|
|
= 1x2x3 … n (n+1)(n+2)…(n+p) / n! |
|
|
|
= (n+p) ! / n! |
|
|
|
= p!
(n+p) ! / (n! p!) |
|
|
|
=
p! (n+p) ! / (n! p!) |
|
|
|
= p! Cpn+p |
|
|
|
(n+1)(n+2)…(n+p)
= p! Cpn+p |
|
|
|
Cpn+p
= (n+1)(n+2)…(n+p) / p! |
|
|
|
(n+1)(n+2)…(n+p)
est divisible par p! |
|
Voir Divisibilité
|
|
||
|
|
|
|
|
|
||
|
|
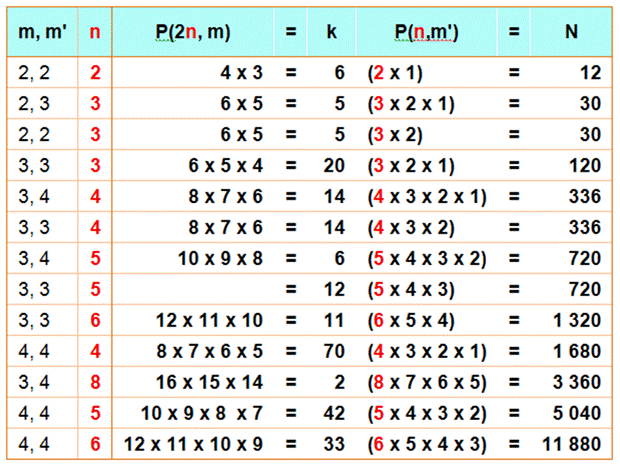
P (n, m) = n (n – 1) (n – 2) …(n – m+1) |
|
|
|
P(k.n, m) = k' P(n, m') |
|
|
|
P(2n, 3) = 2P(n, 4) avec
n = 8 16
x 15 x 14 = 2 (8 x 7 x 6 x 5) = 3 360 |
|
|
P(2n, 2) = k P(n, 2) |
|
|
|
|
4 x 3 = 6 (2
x 1) = 12 6 x 5 = 5 (3
x 2) = 30 |
|
|
|
|
|
|
P(2n, 2) = k P(n, 3) |
|
|
|
|
6 x 5 = 5 (3
x 2 x 1) = 30 |
|
|
|
8 x 7 = 7/3 x (4
x 3 x 2) = 56 |
|
|
|
|
|
|
P(2n, 3) = k P(n, 3) |
|
|
|
|
6 x 5 x 4 = 20 (3
x 2 x 1) = 120 8 x 7 x 6 = 14 (4
x 3 x 2) = 336 10 x 9 x 8 = 12 (5
x 4 x 3) 12 x 11 x 10 = 11 (6
x 5 x 4) = 1 320 |
|
|
|
|
|
|
P(2n, 3) = k P(n, 4) |
|
|
|
|
16 x 15 x 14 = 2 (8 x 7
x 6 x 5) = 3 360 |
|
|
|
10 x 9 x 8 = 6 x 5 x 4 x
3 x 2 = 720 |
|
|
|
8 x 7 x 6 = 14 (4 x 3 x
2 x 1) = 336 |
|
|
|
|
|
|
P(2n, 2) = k P(n, 4) |
|
|
|
Première rationnelle avec k
= 14/3 et n = 4. |
/ |
|
|
|
|
|
|
P(2n, 4) = k P(n, 4) |
|
|
|
|
8 x 7 x 6 x 5 = 70 (4 x 3 x 2 x 1) = 1 680 10 x 9 x 8
x 7 = 42 (5 x 4 x 3 x 2) = 5 040 12 x 11 x 10 x 9 = 33 (6 x 5 x 4 x 3) = 11 880 |
|
|
|
|
|
|
Toutes
les relations du type P(2n, m) = k P(n, m'). On
pourrait considérer P(h.n, m) et poursuivre le tableau.
|
Table des
factorielles tronquées
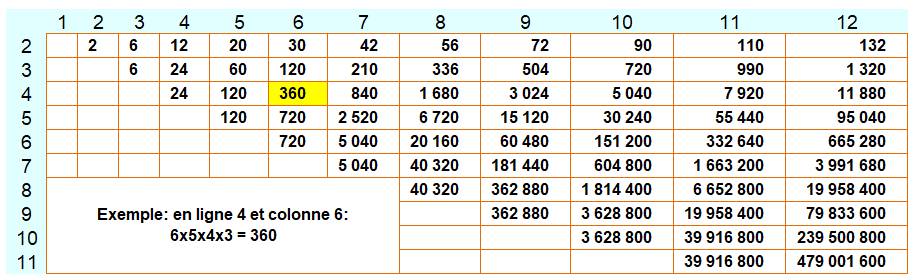
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()