|
|||||||||||||||||||||||||||||||||||
![]()
|
BOÎTES Volume maximum avec une
surface donnée? La réponse n'est pas évidente! |
|
|
||
|
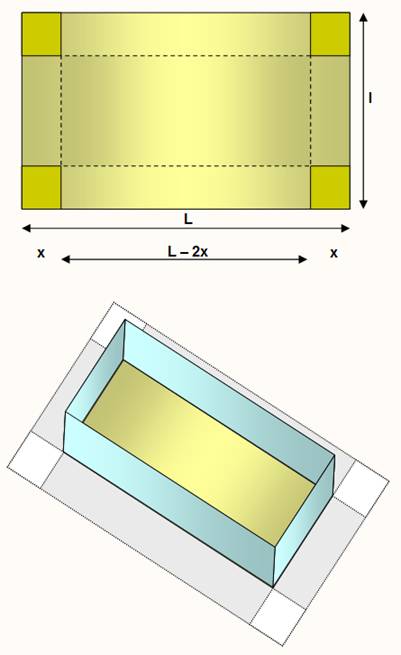
UNE FEUILLE DE PAPIER
LA BOÎTE ET SES DIMENSIONS
|
|
|
|
SOMMES-NOUS À LA DÉRIVE?
La
dérivée de a.xk est a.k x(k – 1) Par
exemple: 4x3 donne
4 . 3 x3-1 = 12x² |
V = 4x3 –
2x² (L + l) + x.L.l V' = 12x² – 4x (L
+ l) + L.l Soit à résoudre une équation du second degré. |
|
|
|||
|
Exemple |
Longueur Largeur |
200 cm 100 cm |
|
|
Résolution de
l'équation du second degré |
Vp = |
12x² – 1200x +
20000 |
|
|
|
Calcul de la
hauteur (x) Longueur de boîte Largeur de boîte Volume |
78, 867 … cm 42, 264 … cm - 57, 735 … Impossible - 192 450,0… cm3 |
|
|
|
Calcul de la
hauteur (x) Longueur de boîte Largeur de boîte Volume |
21, 132 … cm 157, 735… cm 57, 735 … cm 192 450,0… cm3 |
|
|
ILLUSTRATION |
|
||||||||||||
|
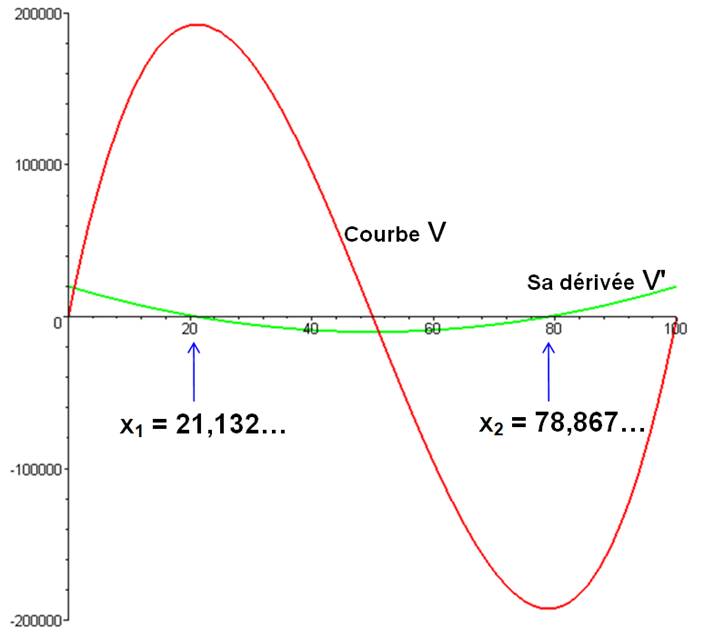
Courbe rouge: V
= 4x3 – 600x² + 20 000x Courbe verte: V' = 12x² – 1 200x + 20 000
Note: On comprend que la deuxième solution soit à rejeter, le
volume (courbe rouge) étant négatif. Quelques autres exemples pour L = 100
|
|||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()