|
|||||||||||||||||||||||||||||||||||
![]()
|
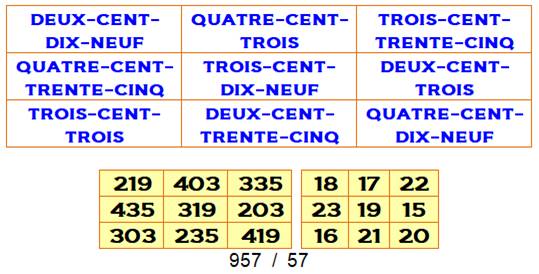
Carrés Alpha-Magiques (CAM) Avec un
carré alpha-magique, le carré de nombres est magique au sens classique (même
somme sur lignes, colonnes et diagonales), et le carré formé avec le nombre de lettres
des nombres est lui-aussi magique. Les nombres utilisés sont consécutifs
(vrais alpha-magiques) ou quelconques (pseudo alpha-magiques). Actuellement
(fin 2017), les références disponibles sur Internet
(sites ou extraits de livres) ne permettent pas d'approfondir le sujet. Cette
page présente un résumé de la question et une recherche personnelle sur les
alpha-magiques d'ordre 3 en français. La
recherche sur ordinateurs est assez simple lorsqu'on a établi la liste des
quantités de lettres des nombres. Voir Tables |
Voir Carrés
magiques 3x3 / Carrés
magiques 4x4
|
Lee Sallows
(né en 1944)
Lee Sallows est un expert en mathématiques
récréatives notamment en carrés magiques. Il est le créateur des carrés alpha-magiques en 1986 suite à lecture
d'un livre datant de 1187: The Origin of Tree Worship. Il est aussi à l'origine des carrés géomagiques. |
|
|
|
|
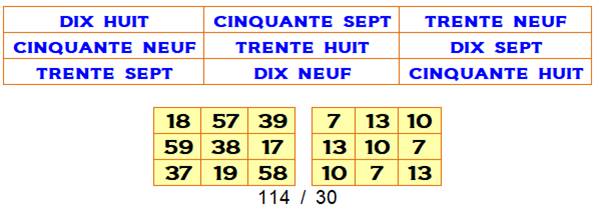
La quantité de lettres pour écrire
les nombres est calculée sans compter les espaces et les traits d'union (no space and no hyphen). Le plus petit SANS
contrainte sur les nombres du second carré
Sans contraintes sur les nombres du
second carré, il y a 510 carrés alpha-magiques d'ordre 3 comportant des
nombres jusqu'à 500. Voir Liste des quantités de lettres pour
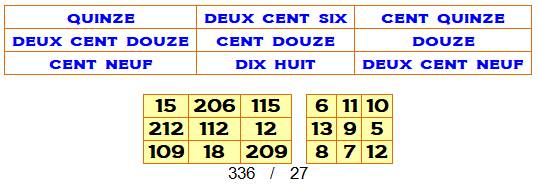
écrire les nombres Le plus petit AVEC
nombres consécutifs dans le second carré
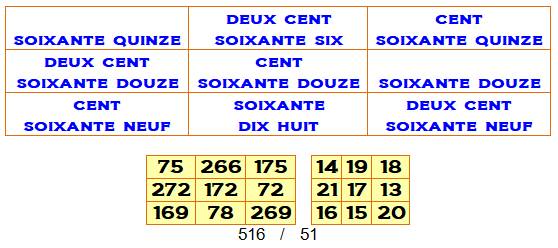
Le suivant, avec un
nombre max = 269 (209 pour le précédent)
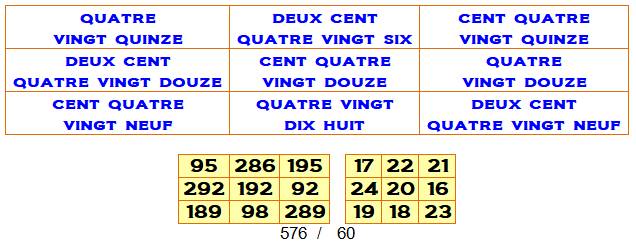
Le suivant exigeant en
amplitude max = 292
Bilan Il y a 42
carrés alpha-magiques avec une amplitude maximale inférieure à 500.
Les nombres sont écrits sans trait d'union et on ne compte pas les espaces.
Le deuxième carré est sous contrainte: les neufs nombres sont consécutifs. |
|
|
|
|
|
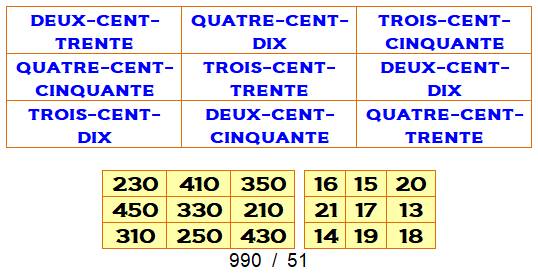
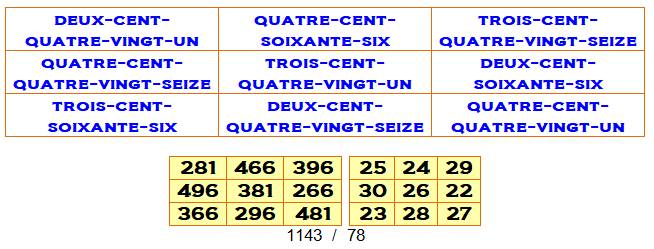
Quantité de lettres pour écrire les
nombres avec la nouvelle orthographe
comportant des traits d'union partout. Quantité équivalente à celle de l'ancienne
orthographe avec espace et traits d'union (with spaces and hyphens). Le plus petit avec
nombres consécutifs dans le second carré
Le suivant exigeant en
amplitude max = 450 (435 pour le précédent)
Le plus grand
inférieur à 500
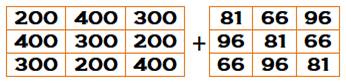
Structure de ces
carrés alpha-magiques: Somme de deux carrés magiques assez
sommaires!
Bilan Il y a 38
carrés alpha-magiques avec une amplitude maximale inférieure à 500.
Les nombres sont écrits avec trait d'union partout conformément à
l'orthographe en vigueur. |
|
Voir Orthographe des
nombres / Quantité de
lettres dans les nombres écrits
Algorithme de recherche des carrés alpha-magiques
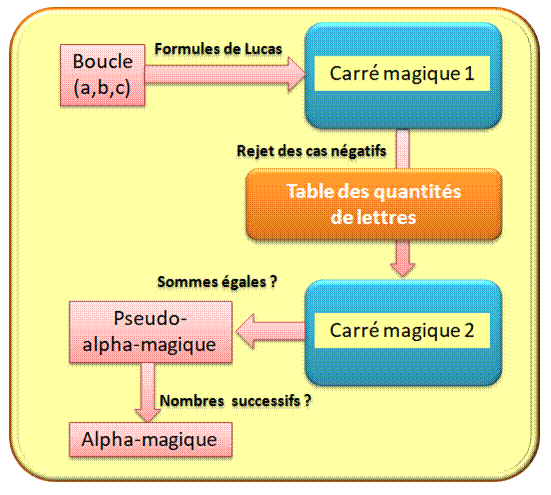
Voir Formule
de Lucas du carré magique d'ordre 3
/ Programmation – Index
![]()
Carrés
alpha-magiques en langue étrangère
|
|
||||||||||||||||||||
|
||||||||||||||||||||
|
Transcription en
chiffres
Constante = 45 |
et en nombre de
lettres
Constante = 21 |
|||||||||||||||||||
|
Ces
deux carrés sont magiques. Et, les
nombres de lettres utilisées sont consécutifs (3 à 11). Harvey Heinz cite cette
curieuse propriété: 100 x carré de gauche + 100 x de
droite = carré magique de constante 666.
Exemple : 105 + 122 + 118 + 104 +109 + 108 = 666 Anglais: alphamagic square, alphamagic
number square, lucky magic square, spell out magic square. |
||||||||||||||||||||
Voir La référence Sallows pour 10 anglo-magiques
3x3
|
|
|
|
Carré doublement alpha-magique (en
cascade) dû à Chris Patuzzo (2017):
|
|
|
|
|
|
Carré anglais alpha-magique
réversible de Peterson Le deuxième carré alphanumérique est
le cousin-miroir du premier: chaque nombre est retourné:
26 devient 82.
Sommes
170 / 39
Sommes
314 / 40 On se souvient qu'il existe de très
nombreux de carrés magiques normaux d'ordre 4
(ceux qui utilisent les nombres de 1 à 16). Les carrés alpha-magiques le sont
également. |
|
Voir Carres
4x4 Inversés
Tous les exemples suivants
sont des pseudo-alpha-magiques
|
|
|
|
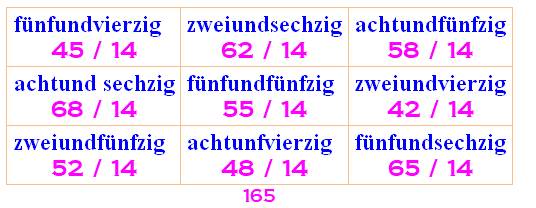
La langue allemande se prête bien à
ce jeu: la majorité des unités ont quatre lettres et les dizaines en ont
sept. Il existe 221 carrés alpha-magiques
3x3 en utilisant les nombres jusqu'à 100.
Le carré avec les nombres de lettres
est plutôt un carré uniforme avec le nombre 14 partout. Cette recherche en allemand est
explicitée dans la livre de Richard Guy et Robert Woodrow
cité en référence. |
|
|
|
|
|
Carré
russo-magique Dans le tableau, on trouve:
Sommes
216 / 36 Le carré en quantité de lettres est
composé des trois nombres 9, 12 et 15. Premier carré russo
magique découvert par Lee B. Croft et Samuel Comi (Université d'état d'Arizona). Ils l'ont baptisé Lee
Sam. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Extraits disponibles sur Internet |
|
|
Liens vers les sites généraux sur les carrés magiques
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/Alphamag.htm |
![]()