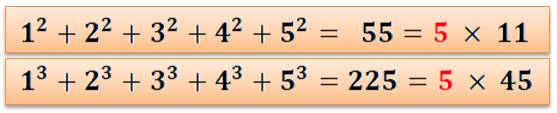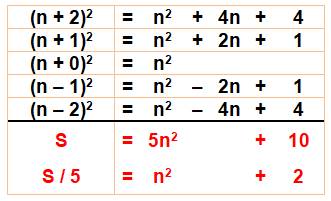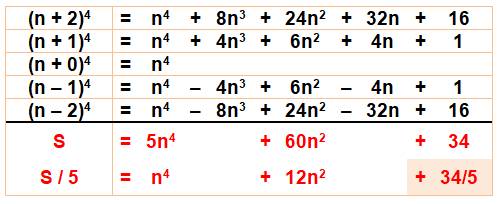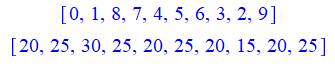NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	DIVISION
Débutants Division	Divisibilité				Glossaire Division
INDEX Décomposition des nombres Sommes de nombres	Index divisibilité		Divisibilité par 5	Critères
			Puissances et divisibilité par 5
		Sommaire de cette page >>> Cinq nombres successifs à la puissance p et divisibilité par 5 >>> Développement des sommes de puissances >>> Expression algébrique divisible par 5 ou non >>> Somme des unités divisible par 5 >>> Table des sommes de cinq puissances successives >>> Bilan pour sommes de 3 à 9 termes

DIVISIBILITÉ par 5

des sommes de puissances

de cinq nombres consécutifs

Ces sommes de cinq puissances sont souvent divisibles par 5. Certaines ne le sont pas. Lesquelles et pourquoi ?

Toutes ces sommes sont divisibles par 5,

sauf pour les puissances en multiples de 4.

Attention: cette divisibilité par 5 ne résulte pas du tout de la présence de cinq termes dans l'addition.

Cinq nombres successifs à la puissance p et divisibilité par 5
La somme de cinq nombres successifs à la puissance p est souvent divisible par 5. Lesquels ne le sont pas ? Deux possibilités pour obtenir une telle propriété: Dans la somme algébrique tous les termes sont divisibles par 5 (5 est en facteur); ou La somme des unités des termes est divisible par 5.	5^1 + 4^1 + 3^1 + 2^1 + 1^1 = 15 = 3 x 5 5^2 + 4^2 + 3^2 + 2^2 + 1^2 = 55 = 11 x 5 5^3 + 4^3 + 3^3 + 2^3 + 1^3 = 225 = 45 x 5 5^4 + 4^4 + 3^4 + 2^4 + 1^4 = 979 Non divisible 5^5 + 4^5 + 3^5 + 2^5 + 1^5 = 4 425 = 885 x 5

Voir Somme de k carrés de nombres consécutifs

Développement des sommes de puissances
p = 2 Sous forme algébrique la somme des carrés de cinq nombres consécutifs s'écrit: S = (n + 2) + (n + 1) + n + (n – 1) + (n – 2) Le tableau montre le développement de cette somme et la mise en évidence du facteur 5. Bilan: divisibilité par 5.
p = 3 En calculant le développement, on retrouve un facteur 5 commun dans le résultat. Cette fois, la somme est non seulement divisible par 5 mais aussi par n. Ce sera le cas pour toutes les puissances impaires. Bilan: divisibilité par 5n.
p = 4 Le résultat avec 4 montre un terme constant (34) non divisible par 5. On tient notre explication !

Expression algébrique divisible par 5 ou non
La suite des formules jusqu'à p = 10 => (somme, sa valeur, et sa division par 5) Divisibilité selon p p = 2 => 5 p = 3 => 5n p = 4 => non p = 5 => 5n p = 6 => 5 p = 7 => 5n p = 8 => non p = 9 => non p = 10 => n Nous allons voir que pour p = 9, en utilisant la seconde méthode ci-dessous les choses changent …

Voir Identités pour puissances supérieures à 2

Somme des unités divisible par 5
Nous cherchons, cette fois, si par hasard, la somme des puissances se termine par 0 ou 5, signe de divisibilité par 5.		En prenant les cinq premiers nombres (0, 1, 2, 3, 4) et l'unité des carrés (0, 1, 4, 9, 6); leur somme est (20). Elle est divisible par 5. On constate (tableau ci-dessous) que toutes les sommes des cinq nombres consécutifs ayant ces unités sont divisibles par 5. En calculant cette somme des unités des carrés dans les dix cas, on trouve effectivement que toutes sont divisibles par 5.
p = 1 Unité des nombres de 0 à 9 et la somme 5 par 5. Toutes ces sommes sont divisibles par 5. Notez que la somme glissante de cinq nombres (jaune) est toujours divisible par 5. Normal: elle commence avec 10 et on ajoute le nombre de tête moins le nombre de queue dont la différence est toujours 5. La somme vaut 5 fois le nombre central.			Nombres unités et somme glissante de cinq Somme glissante de cinq nombres
p = 2 Unité des carrés des nombres de 0 à 9 et la somme 5 par 5. Toutes ces sommes sont divisibles par 5.
p = 3 Unité des cubes des nombres de 0 à 9 et la somme 5 par 5. Toutes ces sommes sont divisibles par 5.
p = 4 Unité des puissances 4 des nombres de 0 à 9. Aucune somme 5 par 5 n'est divisible par 5.
p = 9 Unité des puissances 9 des nombres de 0 à 9. Toutes les sommes sont divisibles par 5.
Conclusion	Cette deuxième recherche confirme la divisibilité pour p = 2 et p = 3; la non-divisibilité par 4 qui demeure; en revanche, pour 9, on avait une non-divisibilité avec la première méthode, mais celle-ci est acquise du fait de la seconde méthode. Les deux méthodes se complètent.

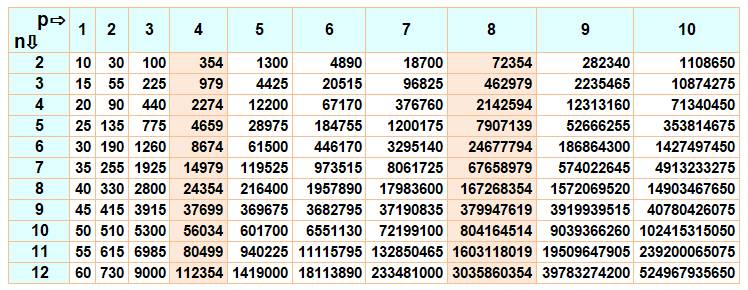
Table des sommes de cinq puissances de nombres successifs

Voir Tables – Index

Bilan
Le tableau donne les couples: [puissance, divisibilité] Divisibilité de la somme de cinq nombres consécutifs portés à la puissance p.	[1, 5], [2, 5], [3, 5], [4, 1], [5, 25], [6, 5], [7, 5], [8, 1], [9, 5], [10, 25], [11, 5], [12, 1], [13, 5], [14, 5], [15, 25], [16, 1], [17, 5], [18, 5], [19, 5], [20, 1], [21, 5], [22, 5], [23, 5], [24, 1], [25, 125], [26, 5], [27, 5], [28, 1], [29, 5], [30, 25], [31, 5], [32, 1], [33, 5], [34, 5], [35, 25], [36, 1], [37, 5], [38, 5], [39, 5], [40, 1], [41, 5], [42, 5], [43, 5], [44, 1], [45, 25], [46, 5], [47, 5], [48, 1], [49, 5], [50, 125], [51, 5], [52, 1], … Seules les puissances divisibles par 4 ne produisent pas des sommes divisibles par 5. Avec les puissances en 5 non multiples de 4, on trouve une divisibilité accrue en 5^k. Les sommes pour p impair sont également divisibles par le nombre central. Exemple 9^7 + 8^7 + 7^7 + 6^7 + 5^7 = 4 782 969 + 2 097 152 + 823 543 + 279 936 + 78 125 = 8 061 725 = 5 x 7 x 230 335 = 5² x 7² x 6 581
Avec deux nombres consécutifs	Aucune divisibilité notable. Ex: 2² + 3² = 4 + 9 = 13, un nombre premier.
Avec trois nombres consécutifs	La somme des puissances p est divisible par 3 pour p impair. Pour p = 9, on a une divisibilité par 27.
Avec quatre nombres consécutifs	La somme des puissances p est toujours divisible par 2 et par 4 pour p impair > 1.
Avec sept nombres consécutifs	La somme des puissances p est toujours divisible par 7 sauf pour p multiple de 6.
Avec huit nombres consécutifs	La somme des puissances p est toujours divisible par 4 et par 4 pour p impair > 1.
Avec neuf nombres consécutifs	La somme des puissances p est toujours divisible par 3 et par 9 pour p impair. Divisible par 27 pour p = 3; par 81 pour p = 9.

Retour	Divisibilité par 5
Suite	Formes polynomiales en général Voir haut de page Sommes des carrés avec nombres consécutifs Sommes de nombres à des puissances successives Divisibilité de la somme des puissances
Voir	Calcul mental – Index Géométrie – Index Nombres parfaits  Théorie des nombres – Index
DicoNombre	Nombre 5 Nombre 30 Nombre 50 Nombre 55 Nombre 90	Nombre 3 367 Nombre 20 196 Nombre 45 045 Nombre 8 061 725 Nombre 574 304 985
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi5P.htm