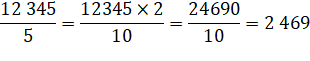collection de nombres, divisibilité par 5

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/03/2022 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
Index général >>> INDEX	Index divisibilité	Divisibilité par 5	Critères
		Puissances et divisibilité par 5
		Sommaire de cette page >>> Divisibilité par 5 ou par 10 >>> Progression arithmétique >>> Somme de cinq nombres divisible par 5 >>> Forme polynomiale en 11 >>> Forme polynomiale en 2 et 3 >>> Divisible par 15 >>>

DIVISIBILITÉ par 5

Critères de divisibilité et formes polynomiales divisibles par 5.

Divisibilité par 5 et 10
Divisibilité par 10	Il suffit que le nombre soit terminé par au moins un 0. Ex: 1 230 = 123 x 10 12 300 = 123 x 100 = 1 230 x 10 1000 = 10 x 100 10^k = 10 x 10^k-1
Divisibilité par 5	Il suffit que le nombre soit terminé par au moins un 0 ou un 5. Ex: 12 345 = 5 x 2 469 123 450 = 5 x 24 690 123 455 = 5 x 24 691 Calcul:
Propriété	Si n est à 0 ou 5 mod 10 alors n est divisible par 5 >>>

Progression arithmétique

La somme de cinq nombres en progression arithmétique est divisible par 5.

La somme de cinq nombres consécutifs est divisible par 5 (cas où k = 1).

Les cinq nombres:

n, n + k, n + 2k, n + 3k, n + 4k

Leur somme:

5n + k + 2 k + 3k + 4 k

= 5n + k (1 + 2 + 3 + 4)

= 5n +10k

Qui est divisible par 5.

Somme de cinq
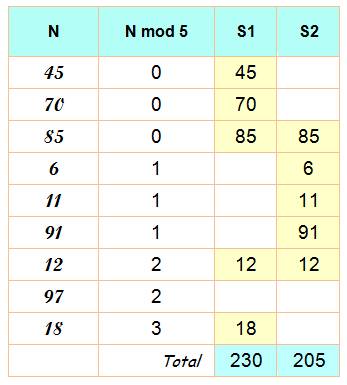
Avec 17 nombres choisis au hasard, il en existe toujours cinq dont la somme est divisible par 5.	Pour être divisible par 5, la somme doit être égale à 0 modulo 5. Les cinq doivent avoir la même valeur modulo 5, ou Les valeurs modulo 5 doivent s'ajouter pour donner 0 modulo 5
Première approche Cinq nombres de même valeur modulo 5 Si cinq nombres ont même valeur modulo 5 (même reste dans la division par 5), leur somme (cinq fois la même valeur) est divisible par 5. Il n'y a que très peu de chance pour que cinq nombres pris au hasard présentent cette propriété. Combien dois-je ajouter de nombres à ces cinq pour être sûr d'avoir une somme divisible par 5? Quatre nombres de même valeur modulo 5 Avec quatre nombres de même valeur modulo 5, le cinquième devra aussi avoir cette valeur pour que la somme soit divisible par 5. La probabilité d'obtenir un cinquième nombre divisible par 5 est fiable. Quatre tels nombres est donc le cas critique. Blocs de quatre nombres de même valeur modulo 5 Le cas supercritique serait que, chaque fois que nous prenons quatre nombres supplémentaires, ils soient de valeurs différentes modulo 5: un bloc de quatre nombres de valeur 0 modulo 5, un bloc de quatre nombres de valeur 1 modulo 5, un bloc de quatre nombres de valeur 2 modulo 5, un bloc de quatre nombres de valeur 3 modulo 5, Avec quatre tels blocs de quatre, il est très probable qu'une somme divisible par 5 se dégage, mais ce n'est pas sûr. Un 17^e nombre fera l'affaire, car: soit il a une valeur modulo 5 qui existe déjà, soit sa valeur ajoutée à quatre autres à sélectionner donnera 0 modulo 5.

Seconde approche

Propriété

Nous avons raisonné sur le cas le plus critique sans compter que la plupart du temps des valeurs peuvent s'ajouter et donner 0 mod 5.

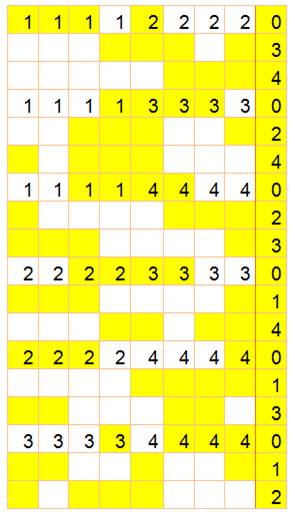
Une inspection des cas possibles montre que:

Parmi 9 nombres pris au hasard, il en existe toujours 5 dont la somme est divisible par 5.

Exemple

Voici dix nombres tirés au hasard puis ordonné selon la valeur du reste de la division par 5 (la valeur du modulo 5).

Nous pouvons y détecter plusieurs sommes de cinq nombres divisibles par 5. Deux exemples (S1 et S2) sont indiqués.

Recherche des configurations critiques

Le tableau ci-contre montre le principe de la recherche. Chaque ligne donne les valeurs modulo 5. (Lire les mêmes nombres sur les lignes non répétées).

Les configurations critiques comportent deux fois quatre nombres dont les valeurs modulo 5 sont identiques. Le cas des valeurs 0 ne sont pas reportées car non critiques (Le 0 étant neutre, il faut moins de nombres pour obtenir la somme 5 ou 10 …).

Sur chaque ligne, on lit la somme cherchée en ajoutant les nombres des cases en jaune.

Dans tous les cas neuf nombres sont suffisants.

Vous pouvez- développer tous les autres cas, avec 3/3/3 par exemple.

Avec 17 nombres (première approche), vous êtes sûr d'obtenir la somme désirée, même beaucoup de somme, mais 8 nombres sont superflus.

Voir Cas de 2, 3 ou 4 nombres

Forme polynomiale en 11
Théorème P(n) = 11ⁿ – 6 est divisible par 5 pour tout n entier. Démonstration
Point de départ	n = 1	P(1) = 11 – 6 = 5 Divisible par 5.
Hypothèse	11^k – 6 11^k	= 5 m = 5 m + 6
Démontrer que sous cette hypothèse	11^k+1 – 6	= 5 m'
En fonction de 11^k		= 11 x 11^k – 6
Valeur supposée de 11^k		= 11 x (5m + 6) – 6
Développement		= 11 x 5m + 66 – 6
Réarrangement et calcul		= 5 x 11m + 60
Factorisation		= 5 (11m + 12) = 5 m'
Induction	Propritée vraie pour k = 1 Propriétée rai pour k + 1 si vraie pour k Alors, toujours vraie.

Voir Démonstration par induction

Forme polynomiale en 3 et 2

Théorème

Démonstration

Divisible par 15

Le produit de cinq nombres impairs consécutifs est divisible par 15.

(n + 1) (n + 3) (n + 5) (n + 7) (n + 9) = 5K pour n pair

Parmi ces cinq nombres, il y en a toujours un divisible par 5 du fait de la présence de cinq facteurs (impairs)

Parmi ces nombres, il y en a toujours au moins un divisible par 3, au pire il est unique est c'est celui du centre.

Exemples

1 x 3 x 5 x 7 x 9 = 945 = 15 x 63

3 x 5 x 7 x 9 x 11 = 10 395 = 15 x 693

5 x 7 x 9 x 11 x 13 = 45 045 = 15 x 3 003

Etc.

Suite	Puissances et divisibilité par 5 Formes polynomiales en général Voir haut de page
Voir	Calcul mental – Index Géométrie – Index Nombres parfaits Théorie des nombres – Index
DicoNombre	Nombre 5 Nombre 3 367 Nombre 45 045
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi5.htm