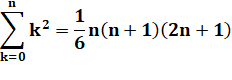|
|||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 6 Nombres et
formes polynomiales divisibles par 6. Règle Un nombre est
divisible par 6 s'il est pair et si la somme de ses chiffres est divisible
par 3. Ex: 123 456 =
3 x 41 152 Propriétés Le produit de trois nombres consécutifs est divisible par 6 >>> Tous les nombres premiers sont voisins d'un multiple de 6 >>> |
Voir Règles
générales / Nombre
6
|
Théorème Tous les nombres de
Fermat sont divisibles par 6. Démonstration On
sait
que: Fn = F0 F1 F2
.... Fn-1 + 2 Avec
F0 = 3: Fn + 1 = 3. F1 F2
.... Fn-1 + 2 + 1
= 3 (F1 F2 .... Fn-1 + 1) Les
nombres de Fermat sont impairs; plus
un donne un nombre pair. Fn + 1 = 3 x 2 x K Donc
divisible par 6. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
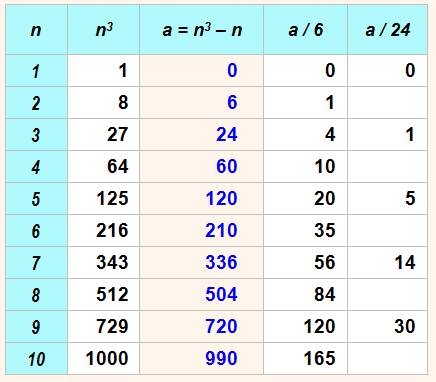
La différence entre deux cubes successifs moins 1 est divisible par 6. Calcul
avec identité
remarquable: En
retirant les extrêmes: 3n² + 3n = 3 n (n + 1) Parmi
deux nombres consécutifs l'un est pair. Leur produit est divisible par 2. L'ensemble
est divisible par 2 et 3, donc par 6. |
Propriété
Tn est le nombre triangulaire
de rang n. Exemples
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec quatre cubes, on obtient une divisibilité
par 12. |
43
+ 33 – 23 – 13 – 10 = 64 + 27 – 8 – 1 – 10 = 72 = 6 x 12 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Théorème Tous les nombres en n3
– n (cad: le produit de trois nombres
consécutifs) sont divisibles par 6 et même par 24
si n est impair. Voir Trois
nombres consécutifs Démonstration n3 – n = n (n² – 1) n (n + 1) (n – 1) (n + 1) n (n – 1) 3 nombres consécutifs L'un d'eux est
forcément divisible par 3 De plus, l'un d'eux, au
moins, est pair Ce nombre est divisible
par 3 et par 2 donc par 6. Propriété
valable pour n3 – n + 6kn Exemple: n3 – n +
6 n = n3 + 5n |
|
Voir Divisibilité
du produit de nombres consécutifs
|
|
|||||||||||||||||||||||||
|
Observations
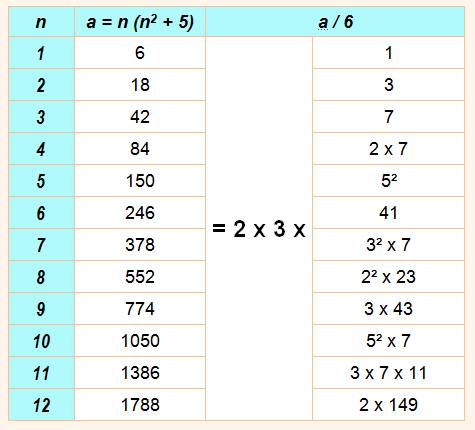
Théorème Tous les nombres en n3
+ 5n sont divisibles par 6. Démonstration Elle a été donnée ci-dessus. Pour l'exercice
reprenons-là. Le nombre est pair
Le nombre est divisible par 3
|
|||||||||||||||||||||||||
Suite en Divisibilité
des formes polynomiales
|
|
||
|
Observations Tableau
donnant n et P le produit n (n + 1) (2n + 1) Puis
P divisé par 6 et ses multiples. En
rouge, les divisions exactes. Somme des carrés des entiers
Voir Démonstration |
n P P/6 P/12 P/24 P/48 P/96 1 6 1 2 30 5 3 84 14 7 4 180 30 15 5 330 55 6 546 91 7 840 140 70 35 8 1224 204 102 51 9 1710 285 10 2310 385 11 3036 506 253 12 3900 650 325 13 4914 819 14 6090 1015 15 7440 1240 620 310 155 16 8976 1496 748 374 187 17 10710 1785 18 12654 2109 19 14820 2470 1235 20 17220 2870 1435 21 19866 3311 22 22770 3795 23 25944 4324 2162 1081 24 29400 4900 2450 1225 25 33150 5525 26 37206 6201 27 41580 6930 3465 28 46284 7714 3857 29 51330 8555 30 56730 9455 31 62496 10416 5208 2604 1302 651 32 68640 11440 5720 2860 1430 715 33 75174 12529 |
|
|
Lecture |
n
(n + 1) (2n + 1) divisible
par 6 toujours divisible
par 12 pour n =
4 k et n = 4k -1 divisible
par 24 pour n =
8 k et n = 8k -1 divisible
par 48 pour n = 16 k et n = 16k -1 etc. |
|
|
Démonstration
de la divisibilité de n (n + 1) (2n + 1) |
|
|
|
Deux nombres consécutifs sont
divisibles par 2, car parmi eux il y a toujours un nombre pair. |
2
|
|
|
Supposons
que n = 3k + r |
n
= 3k + r r
= 1, 2 ou 3 |
|
|
Si n = 3k Cette
expression est divisible par 3. |
n
(n + 1) (2n + 1) = 3k
(3k + 1) (6k + 1) |
|
|
Si n = 3k
+ 1 Cette
expression est divisible par 3. |
n
(n + 1) (2n + 1) = (3k + 1) (3k + 2) (6k + 3) |
|
|
Si n = 3k
+ 2 Cette
expression est divisible par 3. |
n
(n + 1) (2n + 1) = (3k + 2) (3k
+ 3) (6k + 5) |
|
|
Conclusion
pour ces trois cas. Chacun des
cas donne une divisibilité par 3, l'expression est divisible par 3 dans tous
les cas. |
3
|
|
|
Or, elle
est aussi divisible par 2. Elle est
divisible par le produit de ces deux nombre, ou plus exactement, le PPCM de ces deux nombres. |
PPCM
(2,3) = 6 6 |
|
|
Note: La barre verticale veut dire "divise" PPCM Plus Petit Commun
Multiple. |
||
|
|
||
|
Selon le reste de la
division par 6, nous avons 6 cas. |
N = n (n + 1) (n + 5) = n3 + 6n2
+ 5n N = 6 k + {0, 1,
2, 3, 4,
5} |
|
|
N = 6k |
N = 6k (6k + 1)
(6k + 5)
|
|
|
N = 6k + 1 |
N = (6k + 1) (6k + 2) (6k
+ 6)
|
|
|
N = 6k + 2 |
N = (6k + 2) (6k + 3) (6k + 7) = 2 (3k + 1) x 3 (2k + 1) (6k + 7)
|
|
|
N = 6k + 3 |
N = (6k + 3) (6k + 4) (6k + 8) = 3 x (2k + 1) x 2 (3k + 2) x 2 (3k + 4)
|
|
|
N = 6k + 4 |
N = (6k + 4) (6k + 5) (6k + 9) = 2 (3k + 2) (6k +
5) x 3 (2k + 3)
|
|
|
N = 6k + 5 |
N = (6k + 5) (6k + 6)
(6k + 10)
|
|
|
Conclusion |
N = n (n +1) (n + 5) est divisible
par 6 et par 12 pour tous les n sauf n = 2 + 4h (multiple de 4 + 2). |
|
|
Autres du même type |
N = n (n + 4) (n + 5) est divisible
par 6 et par 12 pour tous les n sauf n = 1 + 4h (multiple de 4 + 1). N = n (n + 2) (n + 4) est divisible
par 3. N = n (n + 1) k est toujours divisible par
2. |
|
Voir
Formes comparables / Divisibilité
des formes
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()