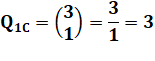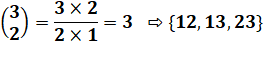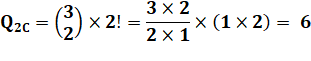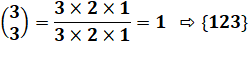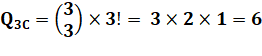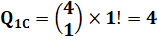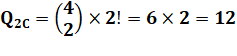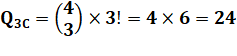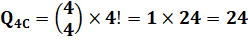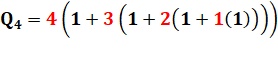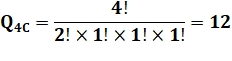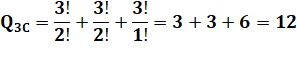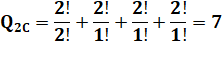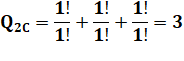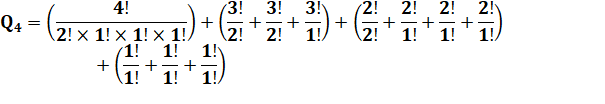|
Édition du: 19/08/2021 |
|
INDEX |
CHIFFRES – Fréquence |
||
![]()
|
Quantité de nombres formés avec les chiffres d'un
nombre ANAGRAMMES des NOMBRES
Compter tous les
anagrammes
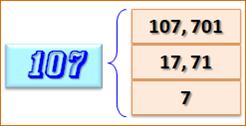
du nombre quelle que soit la quantité de chiffres. Combien parmi eux
sont premiers comme avec 107 (illustration) ? Calculs valables
pour les anagrammes
des mots, sauf en cas de présence de zéros. |
||
|
|
Sommaire de cette page >>>
Approche avec trois chiffres >>>
Récurrence avec quatre chiffres >>>
Cas de répétitions de chiffres >>>
Tables |
Débutants Glossaire |
|
Avec le nombre
123, on peut créer 15 nombres:
|
1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132, 213, 231, 312, 321 |
|
|
Pour un chiffre Choix de
1 par 3 |
|
|
|
Pour deux chiffres Choix de
2 par 3 |
|
|
|
Pour trois chiffres Choix de
3 par 3 |
|
|
|
Pour tous les cas Somme des
trois possibilités |
|
|
|
Avec le
nombre 1234, on peut créer 64 nombres:
|
1, 2, 3, 4, 12, 13, 14, 21, 23, 24, 31,
32, 34, 41, 42, 43, 123, 124, 132, 134, 142,
143, 213, 214, 231, 234, 241, 243, 312, 314, 321, 324, 341, 342, 412, 413,
421, 423, 431, 432, 1234, 1243, 1324, 1342, 1423,
1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421,
4123, 4132, 4213, 4231, 4312, 4321 |
||
|
Pour chacune des quantités de
chiffres |
|
||
|
Total |
|
||
|
Pour le fun |
|
||
|
Avec le
nombre 112, on peut créer 8 nombres:
|
Identification des cas identiques 1, 1', 3, 11', 13, 1'1, 1'3, 31, 31', 11'3,
131', 1'13, 1'31,
311', 31'1 Les rescapés 1, 2, 11, 12,
21, 112, 121,
211 |
|||
|
Avec le
nombre 1123, on peut créer 34 nombres:
|
1, 2, 3, 11, 12, 13, 21, 23, 31, 32, 112, 113, 121, 123, 131, 132, 211, 213, 231, 311, 312, 321, 1123, 1132, 1213, 1231, 1312, 1321, 2113, 2131, 2311, 3112, 3121, 3211 |
|||
|
Pour quatre chiffres Parmi les quatre chiffres, il y a toujours 2 fois
le "1" et une fois les autres. |
|
|||
|
Pour trois chiffres Parmi les trois chiffres, les deux "1"
ne sont pas toujours présents. Il faut examiner les permutations de chaque
combinaison. |
Combinaisons de 3 parmi [1, 1,
2, 3] [112, 113, 134] Permutations sur chacune 3, 3, 6 => 12
|
|||
|
Pour deux chiffres Même type de décompte |
Combinaisons de 2 parmi [1, 1,
2, 3] [11, 13, 14, 34] Permutations sur chacune 1, 2, 2, 2 => 7
|
|||
|
Pour un chiffre Même type de décompte |
Combinaisons de 1 parmi [1, 1,
2, 3] [1, 3, 4] Permutations sur chacune Aucune
|
|||
|
Total |
|
|||
|
Avec ou sans répétition sur un seul chiffre Exemples 123, {1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132,
213, 231, 312, 321}, 15 1123, {1, 2, 3, 11, 12, 13, 21, 23, 31, 32, 112, 113,
121, 123, 131, 132, 211, 213, 231, 311, 312, 321, 1123, 1132, 1213, 1231,
1312, 1321, 2113, 2131, 2311, 3112, 3121, 3211}, 34 1112, {1, 2, 11, 12, 21, 111, 112, 121, 211,
1112, 1121, 1211, 2111}, 13 11112, {1, 2, 11, 12, 21, 111, 112, 121, 211,
1111, 1112, 1121, 1211, 2111, 11112, 11121, 11211, 12111, 21111}, 19 111112, {1, 2, 11, 12, 21, 111, 112, 121, 211,
1111, 1112, 1121, 1211, 2111, 11111, 11112, 11121, 11211, 12111, 21111,
111112, 111121, 111211, 112111, 121111, 211111}, 26 Table
Avec plusieurs répétitions de chiffres Exemples 1122, {1, 2, 11, 12, 21, 22, 112, 121, 122, 211,
212, 221, 1122, 1212, 1221, 2112, 2121, 2211}, 18 11223, {1, 2, 3, 11, 12, 13, 21, 22, 23, 31, 32,
112, 113, 121, 122, 123, 131, 132, 211, 212, 213, 221, 223, 231, 232, 311,
312, 321, 322, 1122, 1123, 1132, 1212, 1213, 1221, 1223, 1231, 1232, 1312,
1321, 1322, 2112, 2113, 2121, 2123, 2131, 2132, 2211, 2213, 2231, 2311, 2312,
2321, 3112, 3121, 3122, 3211, 3212, 3221, 11223, 11232, 11322, 12123, 12132,
12213, 12231, 12312, 12321, 13122, 13212, 13221, 21123, 21132, 21213, 21231,
21312, 21321, 22113, 22131, 22311, 23112, 23121, 23211, 31122, 31212, 31221,
32112, 32121, 32211}, 89 11122, {1, 2, 11, 12, 21, 22, 111, 112, 121, 122,
211, 212, 221, 1112, 1121, 1122, 1211, 1212, 1221, 2111, 2112, 2121, 2211,
11122, 11212, 11221, 12112, 12121, 12211, 21112, 21121, 21211, 22111}, 33 Table
Avec des zéros (élimine des nombres avec des
"0" en tête) Exemples 102, {0, 1, 2, 10, 12, 20, 21, 102, 120, 201,
210}, 11 1002, {0, 1, 2, 10, 12, 20, 21, 100, 102, 120,
200, 201, 210, 1002, 1020, 1200, 2001, 2010, 2100}, 19 10002, {0, 1, 2, 10, 12, 20, 21, 100, 102, 120,
200, 201, 210, 1000, 1002, 1020, 1200, 2000, 2001, 2010, 2100, 10002, 10020,
10200, 12000, 20001, 20010, 20100, 21000}, 29 110, {0, 1, 10, 11, 101, 110}, 6 1102, {0, 1, 2, 10, 11, 12, 20, 21, 101, 102,
110, 112, 120, 121, 201, 210, 211, 1012, 1021, 1102, 1120, 1201, 1210, 2011,
2101, 2110}, 26 11002, {0, 1, 2, 10, 11, 12, 20, 21, 100, 101,
102, 110, 112, 120, 121, 200, 201, 210, 211, 1001, 1002, 1010, 1012, 1020,
1021, 1100, 1102, 1120, 1200, 1201, 1210, 2001, 2010, 2011, 2100, 2101, 2110,
10012, 10021, 10102, 10120, 10201, 10210, 11002, 11020, 11200, 12001, 12010,
12100, 20011, 20101, 20110, 21001, 21010, 21100}, 55 Table
Note: les chiffres 1, 2, 3… sont pris à titre d'exemples, on peut les
remplacer par les autres. 123, {1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132,
213, 231, 312, 321}, 15 246, {2, 4, 6, 24, 26, 42, 46, 62, 64, 246, 264,
426, 462, 624, 642}, 15 789, {7, 8, 9, 78, 79, 87, 89, 97, 98, 789, 798,
879, 897, 978, 987}, 15 159, {1, 5, 9, 15, 19, 51, 59, 91, 95, 159, 195,
519, 591, 915, 951}, 15 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Table
des anagrammes des nombres
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |