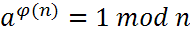|
NOMBRES - Curiosités, théorie et usages Accueil / Dictionnaire / Rubriques / Index / Références / Nouveautés ORIENTATION GÉNÉRALE - M'écrire - Édition du: 27/10/2011 |
|
-Ý- Rubrique: Nombres PREMIERS |
|
|||||
|
§ Records |
|||||||
|
=> Autres
développements sur les nombres premiers |
|||||||
|
NOMBRES PREMIERS
ENTRE EUX |
|||||||
|
Sommaire de cette page >>> PREMIERS ENTRE EUX >>>
SOMME DE PREMIERS ENTRE EUX >>> NOMBRES DE FERMAT |
|||||||
|
NOMBRES PREMIERS ENTRE EUX ou ÉTRANGERS § Nombres qui ne sont pas divisibles l'un par l'autre |
-Ý- PREMIERS ENTRE EUX
|
Théorème
Exemple
|
Démonstration
En fait (ici n = 5) Avec n+1 nombres dans 2n, il y en aura forcément 2 consécutifs donc, premier entre eux Louis Posa |
-Ý- SOMME DE PREMIERS ENTRE EUX
|
Théorème
Exemple avec 5 & 6
|
Numérologie Vers 1900, un chirurgien
berlinois Wilhelm Fliess, ami de
Freund, était obsédé par les
nombres Cycle mâle : 23 jours Cycle femelle : 28
jours En composant ces deux
nombres, il faisait dire ce qu'il voulait à n'importe quel nombre
. Freund écrit que 51 ans, somme de 23 et 28, est l'âge critique de
l'homme Encore récemment, il existe des adeptes de
cette numérologie Note importante Comme l'indique le
théorème cité, tout couple de premiers
entre eux aurait fait
l'affaire ! |
-Ý- NOMBRES
DE FERMAT
|
Deux nombres de Fermat sont premiers entre eux |
|
|
||
|
Suite
en Phi d'Euler |
||
|
Voir |
||
|
|
Aussi |