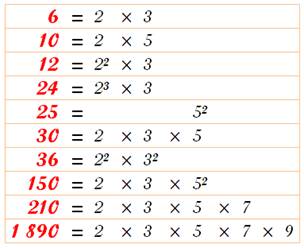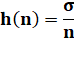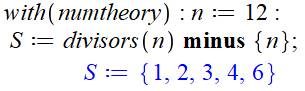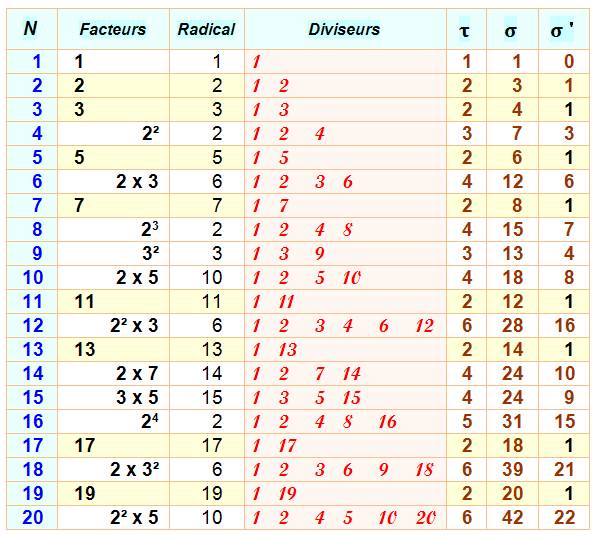
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Diviseurs	DIVISEURS & FACTEURS				Glossaire Diviseur
INDEX Facteurs et diviseurs Divisibilité Décomposition Nombres premiers Types de nombres	Généralités	Calculs	Fact. Premiers	Liste
	2^n Diviseurs	Communs	Records	Théorie >>>
	Plus grand facteur	Composés	Hautement composé	Programmation
	Quantité diviseurs		Somme diviseurs
		Sommaire de cette page >>> Approche >>> Théorème fondamental >>> Définitions >>> Programmation >>> Radical >>> Exemples >>> Diviseurs unitaires >>> Une certaine classification des nombres >>> Chiffres dans les diviseurs – Curiosités

DIVISEURS & FACTEURS

Les diviseurs d'un nombre n sont tous ces nombres qui peuvent le diviser exactement y compris 1 et lui-même. Par exemple, 4 est un diviseur de 12 car 4 x 3 = 12.

Quelques uns de ces diviseurs sont des nombres premiers. Ils suffisent pour caractériser complètement le nombre. Ce sont les diviseurs premiers, communément appelés: facteurs.

Facteurs et diviseurs

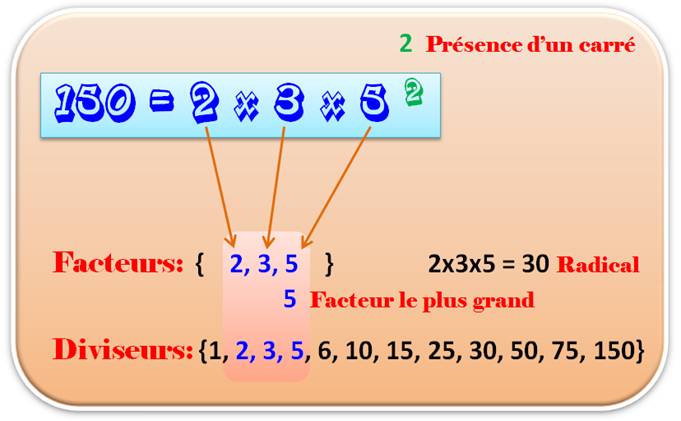
Rappel, vous pouvez accéder à la Page pour débutants / Nombres imagés avec leur facteurs

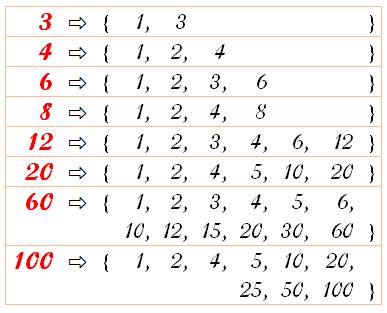
Diviseurs de quelques nombres

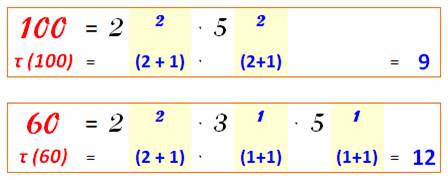
Les diviseurs stricts sont tous les diviseurs sauf le nombre lui-même.

Quantité de diviseurs (tau)

Quantité de diviseurs = produit des exposants incrémentés >>>

APPROCHE

Observations Le nombre 5 = 1 x 5 est Premier car 5 est le produit de 1 par lui-même. Le nombre 15 = 3 x 5 est Composé car 15 est le produit de deux facteurs 3 et 5, autres que 1 et 15. Exemple de nombres composés particuliers Remarquez que le nombre 2 = 1 x 2 est premier; c'est le seul nombre premier pair Note Parfois, notamment pour éviter les problèmes avec les ordinateurs, on pourra trouver d'autres symboles: signe * = multiplication; et signe ^ = élévation à la puissance.

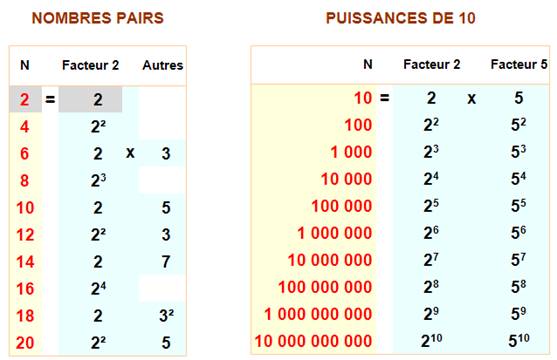
Voir Puissances de 2 / Puissance de 10 / Symboles de la multiplication

Parité avec les nombres impairs

Propriété Tous les diviseurs d'un nombre impair sont impairs. Exemple Div(21) = {1, 3, 7, 21}

Démonstration Un nombre pair est divisible par 2. Si un nombre impair a un diviseur pair, alors ce diviseur est divisible par 2 et, ce nombre 2 fait partie des diviseurs de ce nombre. Ayant un diviseur 2, ce nombre est pair. Ce qui est contraire à l'hypothèse.

Voir Nombres impairs hautement composés

THÉORÈME FONDAMENTAL de l'arithmétique
Théorème Tout nombre est décomposable de façon unique en produit de ses diviseurs premiers, arrangés dans l'ordre croissant. Exemples Remarque Il n'existe qu'une seule manière d'écrire 10 = 2 x 5 avec facteurs croissants. On peut, bien entendu, écrire 10 = 5 x 2 en permutant les facteurs, mais ils ne seraient plus dans l'ordre croissant.

Voir Démonstration / Nombres composés

DÉFINITIONS (en jaune foncé, les notations courantes)
	N	Nombre entier considéré.
	F	Ses facteurs (N est le produit de ces nombres, cette décomposition est unique). >>>
oméga		Quantité de facteurs distincts.
grans oméga		Quantité de totale de facteurs.
lambda zéro		Fonction de Liouville:
		Produit des facteurs distincts.
	D	Diviseurs de N: l'entier N peut être divisé par l'un quelconque de ces nombres).
	D'	Diviseurs propres ou stricts: tous sauf N.
	D^A	Partie aliquote de N: chacun des diviseurs de N sauf 1 et N. Synonyme proche de diviseur propre.
	r	Radical de N: le produit de ses facteurs premiers non répétés. >>>
sigma (comme somme)		Somme des diviseurs de N, y compris N lui-même. >>> Rappel : la lettre sigma majuscule est le symbole de la sommation
		Index du nombre n. Un nombre parfait est un nombre d'index 2.
sigma prime		Somme aliquote de N. Somme des diviseurs stricts de N. Somme des diviseurs de N, sans compter N: ' = – N.
tau		Quantité de diviseurs y compris N. >>>
tau prime		Quantité de diviseurs sans N
phi		Nombre d'entiers inférieurs à N et n'ayant aucun diviseur commun avec N. >>>

Voir Fonctions arithmétiques / symboles / Types de nombres selon les facteurs

Programmation
	Avec le logiciel Maple, ifactor donne la liste de tous les facteurs, factorset, celle des facteurs du radical, divisors, la liste des diviseurs, tau, la quantité de diviseurs, et sigma, leur somme. Rappels: nops donne la quantité d'éléments dans une liste. Le ; demande une impression alors que : permet un calcul interne. restart: efface toutes les mémoires. with(numtheory): appelle des logiciels de théorie des nombres déjà préparés.
	Comment lister les diviseurs propres de n.

RADICAL d'un NOMBRE r(n)
Le radical r d'un nombre entier n est le produit de ses facteurs premiers non répétés. Cad. tous les exposants des facteurs sont positionnés à 1.
Le radical est le plus petit lorsqu'il est la puissance d'un nombre premier	r(p^q) = p r(2) = r(4) = r(16) = r(32) … = 2
Le radical augmente avec la quantité de facteurs premiers.	r(60) = 2x3x5 = 30 = n/2 r(6 948) = 2²x3²x193 = 1 158 = n/6

Voir Tables des radicaux des nombres de 1 à 100 / Programmation / Richesse d'un nombre /

Racine numérique / Calcul de Phi(n) / Conjecture ABC

SUITE ALIQUOTE
Suite formée de la somme des diviseurs d'un nombre, puis la somme des diviseurs du nouveau nombre, etc.	Suite aliquote de 60 60 (60) = 168 (168) = 480 … = 1 512 4 800 15 748 28 672 65 528 122 880 393192

Voir Suite aliquote / Part aliquote

Tables pour les nombres de 1 à 20

Remarques: renseignement sur le nombre selon la somme des diviseurs propres: ' = 1 => N est premier; équivalent à = N+1 => N est premier. C'est le cas des lignes en jaune; par exemple 19 dont la somme des diviseurs vaut 20 et celle des diviseurs stricts vaut 1. >>> ' = N => N est parfait: le nombre est égal à la somme de ses diviseurs stricts. C'est le cas pour le nombre 6. >>> ' < N => N est déficient: la somme des diviseurs stricts n'atteint pas la valeur du nombre; il est abondant dans le cas contraire. C'est le cas pour le nombre 12, le plus petit nombre abondant. >>>

Diviseurs unitaires
Chaque diviseurs d d'un nombre n peut être multiplié par un autre diviseur d', en redonnant le nombre n. d . d' = n	12 est divisible: par 2 et par 6: 2 x 6 = 12 par 3 et par 4: 3 x 4 = 12
Lorsque les deux facteurs du produit ( d et d') sont premiers entre eux, ces diviseurs sont unitaires.	Parmi les diviseurs de 12, les nombres 3 et 4, premiers entre eux, sont des diviseurs unitaires.

Voir Nombres unitairement parfaits

Une possible classification des nombres

Premiers
Un nombre premier n'a que deux diviseurs: un et lui-même, comme le nombre 5;

Semi-premiers

Un semi-premier est le produit de deux nombres premiers. Ex: 15 = 3 x 5.

Multiplications Multiples

Tous les autres sont des nombres à "multiplications multiples" ou à "multiplications ambigües". Ces nombres comportent six diviseurs ou plus et ils peuvent être décomposées en deux produits ou plus. Ex: 12 = 2 x + = 3 x 4

Voir Table des nombres à multiplications multiples

Chiffres dans les diviseurs – Curiosités
Le plus petit pannumérique sans 0 Quel est le plus petit nombre qui contient au moins une fois tous les chiffres de 1 à 9 ? Le plus petit pannumérique avec 0 Quel est le plus petit nombre qui contient au moins une fois tous les chiffres de 0 à 9 ?	54 = 2 x 3^3 Diviseurs: {1, 2, 3, 6, 9, 18, 27, 54} 108 = 2^2 x 3^3 Diviseurs: {1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108}
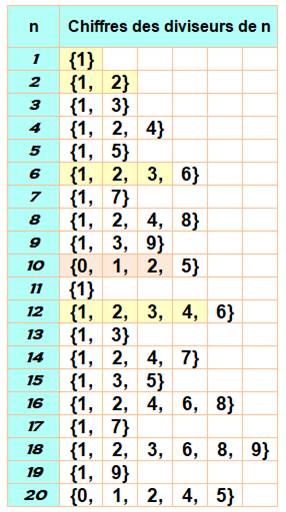
Liste des chiffres des diviseurs de 1 à 20 En jaune, les plus petits avec de plus en plus de chiffres qui se suivent. En ocre, même chose mais en incluant le 0. Records sans le 0 2 – {1, 2} 6 – {1, 2, 3, 6} 12 – {1, 2, 3, 4, 6} 52 – {1, 2, 3, 4, 5, 6} 54 – {1, 2, 3, 4, 5, 6, 7, 8, 9} Records avec le 0 10 – {0, 1, 2} 30 – {0, 1, 2, 3, 5, 6} 60 – {0, 1, 2, 3, 4, 5, 6} 102 – {0, 1, 2, 3, 4, 5, 6, 7} 108 – {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Voir Pannumérique

Suite	Records Types de nombres selon leurs diviseurs Voir en haut de page Connaissant la somme des diviseurs, trouver le nombre Liste des nombres et leurs facteurs et diviseurs Multiensemble et factorisation des nombres Facteurs et diviseurs avec Maxima (programmation) Facteurs avec Scratch (programmation) Multiples et diviseurs sur un chemin eulérien
Voir	Calcul mental – Index Conjecture ABC Diviseurs – Développements théoriques Diviseurs – Somme en puissance Divisibilité Fonctions arithmétiques Géométrie – Index Machine des frères Carissan Nombres composés Nombres hautement composés Nombres parfaits PGCD Premiers Théorie des nombres – Index Types de nombres selon leurs diviseurs
DicoNombre	Nombre 54 Nombre 108 Nombre 114
Site	Factorization using the Elliptic Curve Method – Programme en ligne qui donne les facteurs des nombres
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Sigma.htm

Renvois de liens

Recherche du plus grand nombre de diviseurs >>>

Nombres composés successifs à 3 et 4 diviseurs >>>

Nombres composés jumeaux >>>

Factorielles >>>