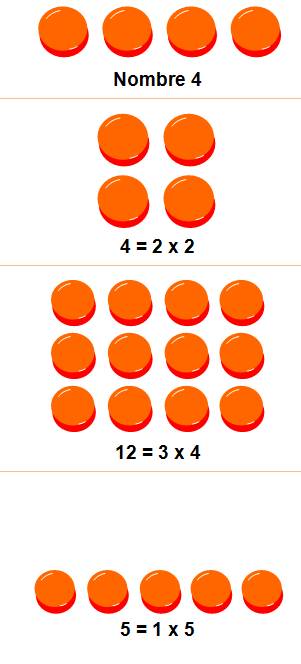|
|||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PREMIERS Initiation
Les nombres
premiers sont les briques de l'arithmétique. |
|
Pour une première idée |
|
|
|
Première
vision
|
Exemples :
6 et 10 sont des nombres composés. 7 et 11 sont des
nombres premiers. |
|
|
Deuxième
vision
|
Exemples
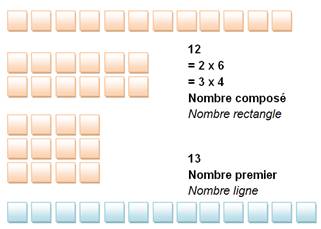
Avec 12, je peux faire une ligne de
12, mais aussi 3 rangées de 4, et même 2 rangées de 6.
Avec 13, je forme simplement une
ligne de 13 pions, Impossible de former un rectangle. |
|
Voir Opération Pénélope
Voyons
cela pas à pas …
|
|
||
|
file
indienne
|
|
|
|
Conclusions
de ces observations: COMPOSÉS
ET PREMIERS |
|
|
|
Les
nombres
Comme 4, 12 , 20 … sont
les nombres COMPOSÉS
Voir Nombres composés |
Les
nombres
sont
les nombres PREMIERS
Voir Nombres premiers |
|
|
|
|
|
Illustration
crible d'Ératosthène
Ce procédé de
tri est connu comme le crible d'Ératosthène, savant grec
qui l'inventa deux siècles avant Jésus-Christ. Anglais: Eratosthene sieve. |
|
Voir Programmation du crible d' Ératosthène / Ératosthène / Primalité
/ Crible de Moessner
|
Analogie
qui trouvera son utilité dans la suite |
|
|
|
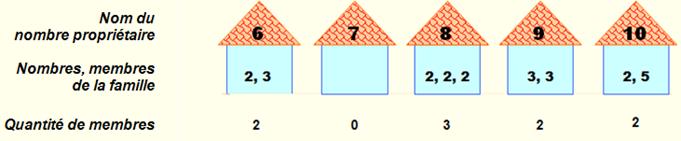
Certains
ne logent personne: les premiers; D'autres
y logent leur famille: les composés.
|
||
|
|
|
|
Voir aussi Les nombres pliés
|
|
|||
|
|
210 = 6 x 35 210 = 2 x 3 x 35 210 = 2 x 3 x 5 x 7
Aux permutations des facteurs près.
Comme 210 = 2 x 3 x 5 x 7 = 3 x 2 x 7 x 5 =… Chaque nombre premier peut être
répété. Comme dans 16 = 2 x 2 x 2 x 2 = 24 |
||
|
Conséquence Les nombres premiers sont les briques de
construction de tous les nombres entiers. Ils sont comparables aux éléments de la
chimie et aux particules
de la physique. Historique Ce théorème était connu des mathématiciens de l'Antiquité. Euclide le connaissait bien, certes
formulé d'une autre manière. Cette propriété a semblait évidente pour
beaucoup et cela a duré bien longtemps. La première démonstration rigoureuse du théorème
attendra Gauss en 1801. Suite
en Historique |
|||
|
|
|
|
Dans le roman Contact de Karl Sagan, l'héroïne,
Ellie Arroway travaille au SETI (Search for Extra Terrestrial Intelligence).
Elle est à la recherche des intelligences extraterrestres. Un jour elle
reconnaît un signal composé de deux pulsations puis rien, puis trois
pulsations, pause, cinq, pause, sept, pause … et cela jusqu'à 907. Elle est
sûre que seuls des êtres intelligents sont capables de créer une telle suite
de signaux représentant les nombres premiers. |
|
Humour
|
Vous
connaissez désormais le début de la liste des nombres premiers: 2, 3, 5, 7,
11, 13 … Voici ce qu'en pense divers spécialistes avec humour: Mathématicien:
3 est premier, 5 est premier, 7 est premier et par induction tous les nombres impairs sont premiers. Scientifique:
3 est premier, 5 est premier, 7 est premier, 9 est sans doute une erreur
expérimentale, 11 est premier … Ingénieur: 3 est premier, 5 est
premier, 7 est premier, 9 est premier, 11 est premier … Informaticien:
3 est premier, 5 est premier, 7 est premier, 7 est premier, 7 est premier … Commercial: 3 est premier, 5 est
premier, 7 est premier, pour 9 pour allons faire pour le mieux. Commercial en informatique:
3 est premier, 5 est premier, 7 est premier, 9 sera premier lors de la
prochaine version. Juriste: 3 est premier, 5 est
premier, 7 est premier, pour 9 il n'y a pas assez de preuve pour annoncer
qu'il n'est pas premier. Contrôleur de gestion:
3 est premier, 5 est premier, 7 est premier, pour 9, il est premier avec la
taxe de 10% et 5% de diverses autres
obligations. Statisticien:
avec une sélection au hasard: 17 est premier, 23 est premier, 11 est premier… Professeur:
3 est premier, 5 est premier, 7 est premier, la suite est laissée comme
devoir à la maison. |
Voir Pensées & humour
![]()
|
Voir |
|
|
|
|
|
|
|
|
Cette page |
![]()