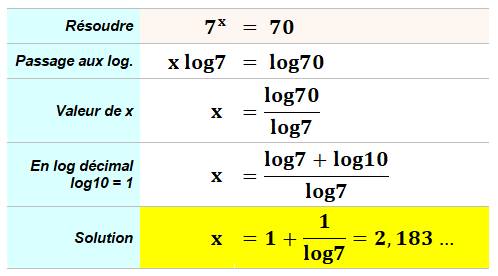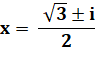Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 17/09/2023 M'écrire Brèves de Maths

INDEX Algèbre Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	50^99 et 99!	Somme de la diagonale
	Divers défis 01	Divers défis 02	Fourmi sur un pavé
	Divers défis 03	Divers défis 04	Demi-cercle et rectangle

Divers défis mathématiques Problèmes rencontrés sur le Net proposés comme défis aux Internautes.
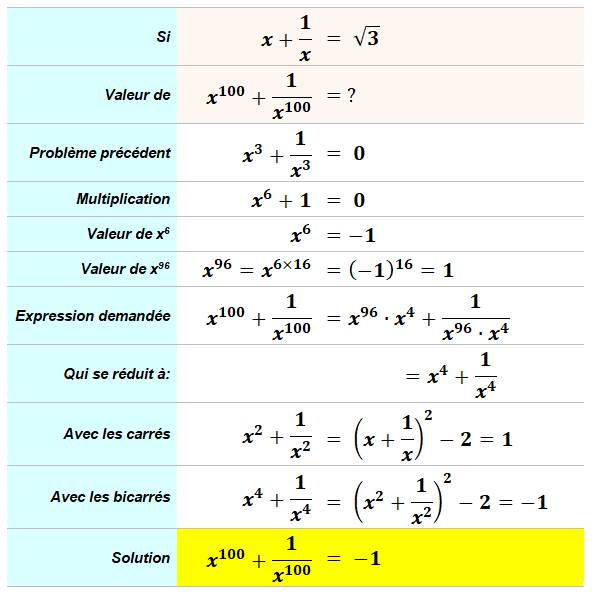
	Sommaire de cette page >>> Différences de 1 à 6 >>> Résoudre cette équation: 7^x = 70 >>> Résoudre cette équation: x + x^2 + x^3 = … >>> Calculer cette expression sous hypothèse; x^18 + x^12 + x^16 + x >>> Calculer cette expression sous hypothèse x^100 + 1/x^100	Débutants Nombres Glossaire Nombres

Différences de 1 à 6		haut
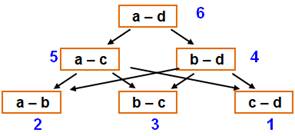
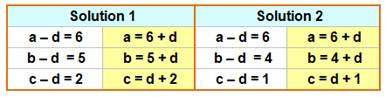
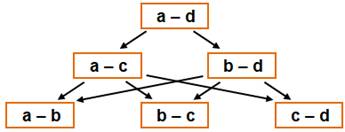
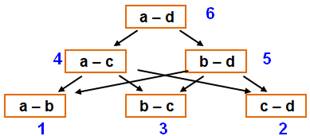
Problème Quatre nombres entiers différents: a, b, c et d. La valeur absolue de leur différence deux à deux. On obtient six nombres entiers: 1, 2, 3, 4, 5 et 6. Valeurs de a, b, c et d ? Solution Les nombres sont tous différents: prenons a > b > c > d. Alors, la plus grande différence est a – d, et elle vaut 6. Les autres relations d'ordre sont indiquées sur le dessin de droite. Les valeurs 1, 2 et 3, les plus petites, sont nécessairement à l'étage du bas. Les valeurs 4 et 5 sont donc à l'étage intermédiaire. Ce qui conduit aux deux solutions présentées à droite. 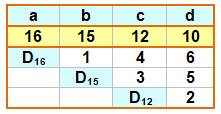Bilan Exemple avec d = 10	Relation d'ordre La flèche signifie: strictement plus grand Deux solutions

Voir Brève 51-1019

Résoudre cette équation: 7^x = 70	haut

Résoudre cette équation: x + x^2 + x^3 = 99 + 99^2 + 99^3	haut
La solution réelle semble évidente après coup ! Mais pouvait-on imaginer qu'elle était la seule réelle ? Et qu'il y avait deux solutions complexes ? En tout cas joli exercice de manipulation d'expressions algébriques.

Voir Équation du second degré

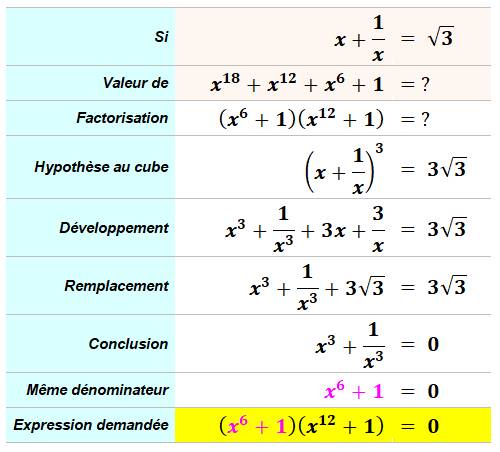
Calculer cette expression sous hypothèse x^18 + x^12 + x^16 + x = ?	haut
Pour information les racines de l'équation en hypothèse sont:

Calculer cette expression sous hypothèse x^100 + 1/x^100 = ?	haut

Haut de page

Retour	Algèbre – Index Énigmes – Index Brèves – Index
Suite	20 défis de géométrie Tests de géométrie Divers défis 02 Équation en x^4 Rectangle et triangle rectangle Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/Defis04.htm