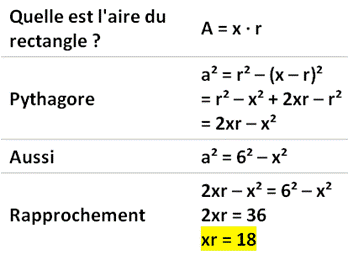|
Édition du: 27/01/2025 |
|
INDEX |
Problèmes – Défis |
||
|
Divers défis
01 |
Divers défis
02 |
||
|
Divers défis
03 |
Divers défis
04 |
||
![]()
|
Divers défis mathématiques Problèmes
rencontrés sur le Net proposés comme défis aux Internautes. |
||
|
|
Sommaire de cette page >>>
Le cercle exinscrit au triangle isocèle >>>
Le cercle, un diamètre et une tangente >>>
Deux cercles dans un triangle rectangle >>>
Rectangle et demi-cercle |
Débutants Glossaire |
|
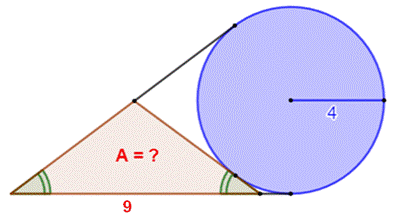
Construction Un cercle de rayon 4 cm et ses tangentes issues
d'un même point. Un triangle isocèle logé dans l'angle entre les
tangentes. Sa base mesure 9 cm. Quelle est l'aire de ce triangle ? Piste La hauteur h semble de même longueur que le rayon
du cercle. L'aire du triangle serait: A = ½ 9 × 4 = 18 cm² Dans ce cas, il faut démontrer que le point F est
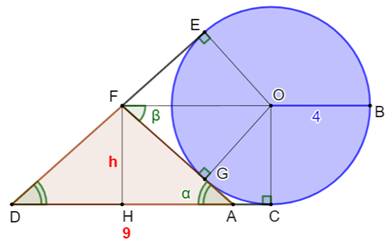
sur la droite OB. Alignement Les segments de tangentes FE et FG sont de même
longueur. Les triangles rectangles FEO et FGO sont
isométriques (égaux). Les angles EFO et GFO sont égaux (β). En F, on a: angle AFD = 180° – 2β . Avec le triangle isocèle AFD, on a également:
angle AFD = 180° – 2α En comparant, on conclut que: α = β
et que FO est parallèle à DC et que les points F, O et B sont alignés. |
Figure initiale (échelle respectée)
Figure annotée
|
|
Voir Cercle
exinscrit et calcul de leur rayon
|
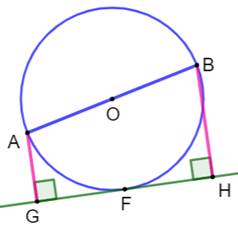
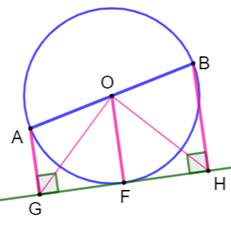
Problème Un cercle et un diamètre AB. La tangente en un point F du cercle. Les perpendiculaires AG et BH à la tangente. Démontrer que OG
= OH. Solution On trace OG, OF et OH (figure du bas). GH est la tangente en S, alors le rayon OF est
perpendiculaire à cette tangente. De ce fait AG, OF et BH, perpendiculaires à GH,
sont parallèles. Avec AO = OB = R, la même proportion se trouve
sur la sécante GH, soit: GF = FH Dans les triangles rectangles OFG et OFH, on a:
Les deux triangles sont donc isométriques et, leur troisième
côté ont même longueur:
|
|
|
|
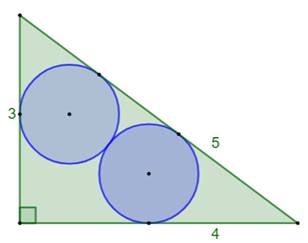
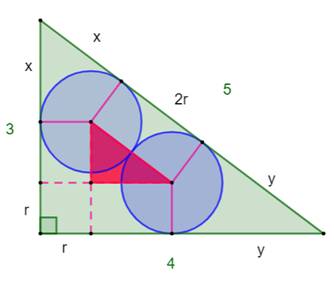
Problème Un triangle rectangle et deux cercles identiques,
tangents entre eux et avec l'hypoténuse. Rayon des cercles ? Solution Voir les
notations sur la figure.
|
|
|
Voir Triangle
3-4-5
|
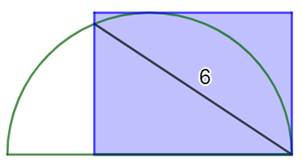
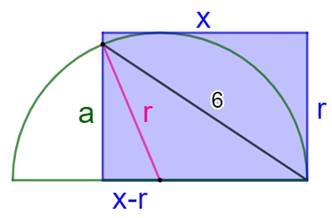
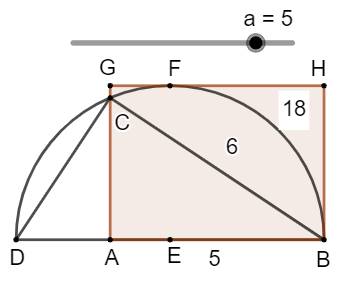
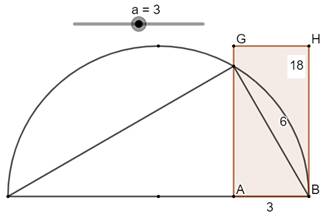
Problème Un demi-cercle et un rectangle. Le segment indiqué mesure 6 cm. Quelle est l'aire du rectangle ? Solution Voir les
notations sur la figure.
|
|
|
|
Commentaires Pour r = 6, l'aire est constante (18) en faisant
varier la longueur de AB = a. Construction de la figure (GeoGebra) Curseur a. Segment AB de longueur a. Cercle de centre B et de rayon 6. Intersection C. Segment AD de longueur: b = (r² – a²) / a. Demi-cercle de diamètre BD. Perpendiculaire en E milieu de BD. Intersection
F. Parallèle en F à BD. Perpendiculaires en A et B à BD; Intersections G
et H. Quadrilatère ABHG. En faisant varier le curseur a, le rectangle se
déforme mais son aire est constante. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/Defis03.htm
|