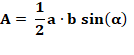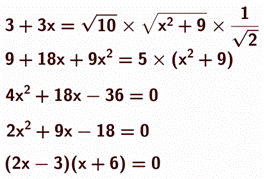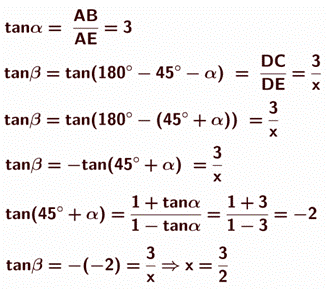Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 20/01/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Double triangle rectangle
	Nappe sur table	Triangle rectangle partagé	Rectangle et triangle
	Carré oblique	Carré et triangle équil.	Triangles dans triangle
	Triangle dans quadrilatère	Trapèze et triangle	Trois triangles réunis

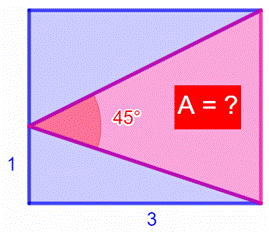
Rectangle et triangle Petit exercice simple pour commencer. Calculer une longueur. Un triangle est inscrit dans le rectangle. Compte tenu des mesures données, calculer la valeur des angles du triangle.
	Sommaire de cette page >>> Rectangle et un triangle rectangle >>> Le triangle dans le rectangle >>> Triangle 45° dans rectangle	Débutants Géométrie Glossaire Géométrie

Rectangle et un triangle rectangle		haut
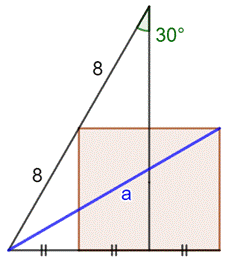
Construction Un triangle rectangle dont l'hypoténuse mesure 2×8 cm et l'un des angles mesure 30°. Un triangle rectangle moitié sur lequel est construit un rectangle comme indiqué sur la figure. Quelle est la longueur du segment bleu ? Piste Avec un angle de 30° dans le triangle rectangle, la longueur de son petit côté est égale à une demi-fois celle de l'hypoténuse. Les triangles rectangles et le théorème de Pythagore feront le reste. Calculs	Figure initiale Figure avec notations

Le triangle dans le rectangle		haut
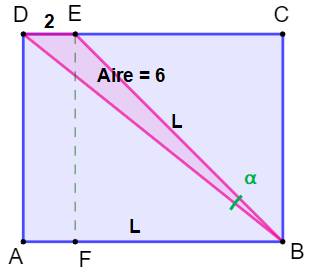
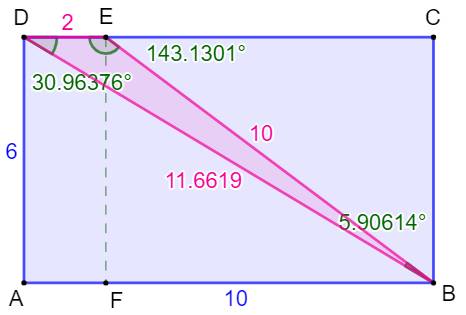
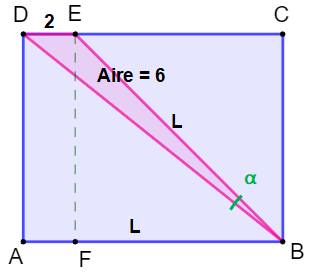
Construction Un rectangle ABCD. Le point E sur DC à 2 cm du point D. L'aire du triangle BDE est égale à 6 cm². On sait que AB = BE = L Quelle es la valeur de l'angle alpha ? Piste Typiquement une situation passible du théorème de Pythagore avec les triangles rectangles ABD ou BFE. Autre piste: l'aire d'un triangle vaut: Connaissant l'aire et la longueur des côtés, il est possible d'en déduire la valeur de l'angle.
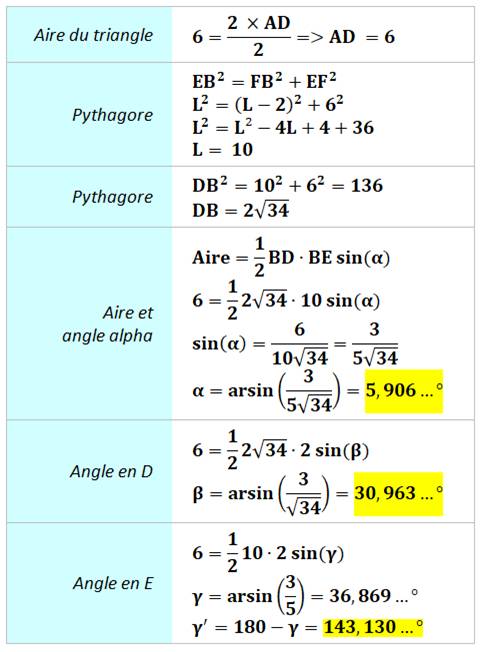
Calculs

Illustration avec GeoGebra

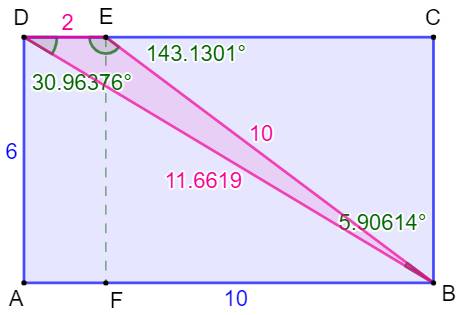
Voir GeoGebra

Triangle 45° dans rectangle		haut
Un peu de Pythagore et calcul de l’aire du triangle par la méthode classique comparée au calcul par le sinus de l’angle. Une seconde méthode exploite le calcul des tangentes des angles.
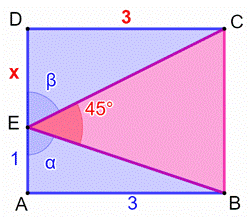
Construction Un triangle rectangle, dont les côtés de l’angle droit mesurent 1 cm et 3 cm, est inscrit dans un rectangle. L’un des angles du triangle rose vaut 45°. Quelle est son aire ? Pistes (Figure du milieu) Dans les triangles rectangles ABE et DCE : EB² = 1² + 3² = 10 EC² = x² + 3² Deux façons de calculer l’aire du triangle BCE : Classique : ABCE = 1/2 × 3(1 + x) Avec sinus : ABCE = 1/2 EB · EC sin45° En égalisant (et en multipliant par 2) : 3 + 3x = √10 × √(x² + 9) × 1/√2 Calcul de x et de l’aire En mettant l’expression au carré : Après factorisation (en remarquant que 3+6+9 et 3×9=18) ou en calculant la racine, on trouve la racine positive : x = 3/2 (l’autre racine qui est négative (-6) est un artefact lié à l’élévation au carré). Aire du triangle : ABCE = 1/2 × 3(1 + 3/2) = 15/4 = 3,75 cm² Résolution par les angles alpha et bêta	Figure initiale Figure avec notations Avec les angles

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/TrgRect.htm