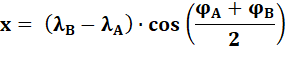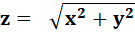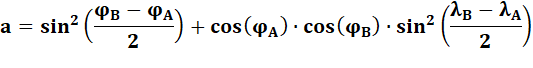|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Distance entre deux points géographiques connus par leurs latitudes et
longitudes Présentation de trois
méthodes. Classiquement pour un lieu
donné:
|
Voir Alphabet
grec
Données pour
les exemples numériques
|
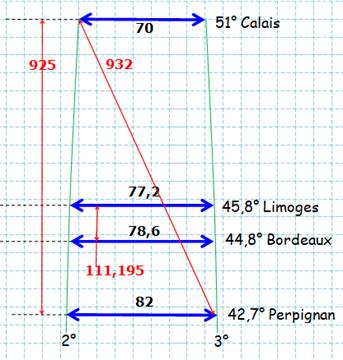
Valeurs pour la France
pour une tranche de longitudes entre 2° et 3°. Les valeurs indiquées (en km) ont
été relevées sur les cartes IGN (GéoPortail)
Lire:
latitude "au niveau" de la ville de Calais, etc. Exemple de lecture:
un degré de longitude à la latitude de Limoges vaut 77,2 km. |
Voir Taille
de la Terre / France
|
|
|||
|
Pour de
petites distances
la méthode utilisant le théorème
de Pythagore marche bien. On calcule x et y des distances exprimées en
degrés (degrés décimaux). Puis, z la distance cherchée exprimée en
"degrés". Le facteur k rétablit l'échelle en kilomètre en
sachant que 1 minute d'arc = 1 mille marin = 1852 m; à multiplier par 60 pour passer
aux degrés. |
Formules
Exemple pour 1° de longitude à la latitude 51° x = 1° × cos (51) = 0,629… y = 0° z = 0,629… d = 1,852 x 60 × 0,629 = 69,9300… km |
||
|
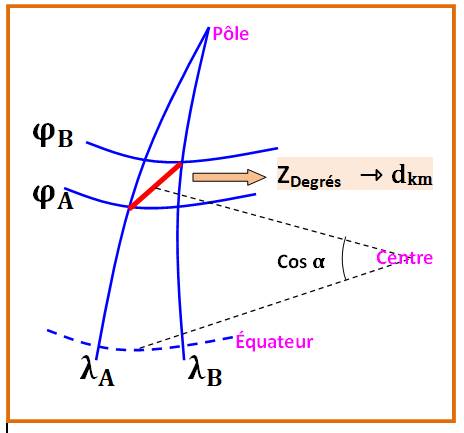
Principe du calcul en image |
|
||
|
Méthode avec loi des sinus |
|
|
La formule donne le cosinus
d'un angle à multiplier par le rayon terrestre.
Exemple pour 1° de longitude à la latitude 51°
d = 6 371 × arccos(0,99993968…) = 69,97 km |
|
Voir explication du calcul en Comment
obtenir la distance entre deux points
connus en longitude et latitude sur la sphère ? –
IGN
|
|
||
|
Cas particulier d'une loi de
la géométrie sphérique, la loi de haversine permet de calculer la distance du
grand cercle entre deux points d'une sphère.
Exemple pour 1° de longitude à la latitude 51° a = 0,000030159… c = 0,010983… d = 69,9767 … km |
||
|
Note: certains
sites donnent c avec atan2: ce n'est pas le
carré, mais l'indication que deux arguments suivent. |
|
|
Merci à Loïc Lafon
Bilan des résultats selon la méthode
|
En km |
D51/1 |
D42,7/1 |
D51 à 42.7 |
|
Cartes IGN1 |
70 |
82 |
925 |
|
Simple |
69,93 |
81,66 |
922.3 |
|
Loi des sinus |
69,97 |
81,72 |
922,92 |
|
Haversine |
69,9767 |
81,7183 |
922,9179 |
1 Par
pointage manuel (on peut sans doute faire mieux en jouant sur l'échelle)
|
|
||
|
|
Commentaires Programmation et résultats pour les trois méthodes. Notez le passage des angles de degrés décimaux en radians. Autres outils S'agissant de la transcription de formules, il est possible très
simplement de passer à un autre langage de programmation ou d'implémenter ces
formules sur un tableur du type Excel. |
|
|
Confirmation avec un calculateur en ligne
Calculate distance, bearing and more
between Latitude/Longitude points – Movable Type Scripts |
||
Grand merci à Walter M.
professeur à Poitiers
![]()
|
Retour |
||
|
Voir |
|
|
|
Livres |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()