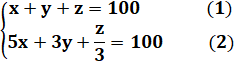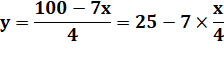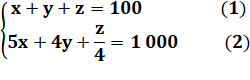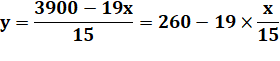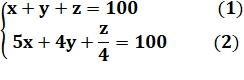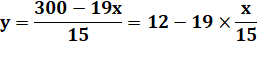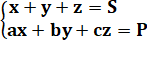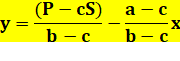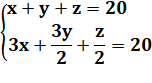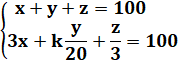|
||||||||||||||||||||||||||||
![]()
|
Énigme: coqs, poules et poussins Problème des cent volailles Combien
de chacune des volailles pour un prix donné? Résolution
avec système d'équations. Très vieux problème chinois du Ve siècle de Zhang Qiujian
et son texte de problèmes mathématiques: Zhang Qiujian suanjing (Le classique
mathématique de Zhang Qiujian). Ce problème, le numéro 38, a été repris dans
les textes indiens et arabes du Moyen Âge. Un des premiers exemples de
problème indéterminé dans l'histoire des mathématiques. Le texte ne donne pas
la méthode de résolution. |
Anglais: Chicken
problems / the hundred fowls problem
|
|
||
|
Énigme J'ai acheté 100 animaux pour 100 euros dont des coqs à 5 euros pièce,
des poules à 3 euros et des poussins à 1/3 d'euro. |
Mise en équation
|
|
|
Anglais If a
rooster is worth five coins, a hen three coins, and three chickens together
are worth one coin, how many roosters, hens, and chickens totaling 100 can be
bought for 100 coins? Rédaction avec monnaie chinoise Now
one cock is worth 5 qian, one hen 3 qian and 3 chicks 1 qian. It is required
to buy 100 fowls with 100 qian. In each case, find the number of cocks, hens
and chicks bought. |
||
|
Résolution (2) x 3 => |
|
|
|
(1) dans (3) => D'où, on conclut que x est un multiple de 4 et x < 16 |
|
|
|
QUATRE
solutions en nombres entiers |
x = 0 y = 25 z = 75 x = 4 y = 18 z = 78 x = 8 y = 11 z = 81 x = 12 y = 4
z = 84 |
|
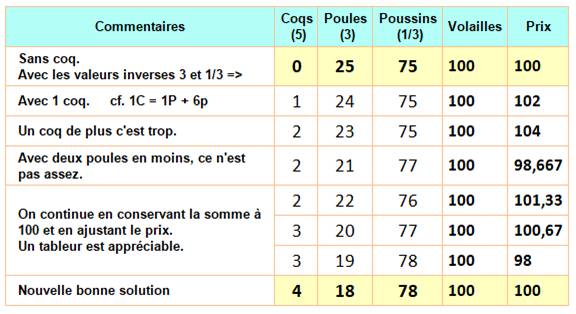
Sans l'algèbre, par essais et corrections
|
|
||
|
Énigme J'ai acheté 100 animaux pour 1 000 euros dont des coqs à 5 euros
pièce, des poules à 4 euros et des poussins à 1/4 d'euro. |
Mise en équation
|
|
|
Résolution (2) x 3 => |
|
|
|
(1) dans (3) => |
|
|
|
PAS
de solutions en nombres entiers |
x = 0
y = 250 z = -160 x = 15 y = 241 z = -156 Impossible de rendre z positif ! |
|
|
|
||
|
Énigme J'ai acheté 100 animaux pour 1 000 euros dont des coqs à 5 euros
pièce, des poules à 4 euros et des poussins à 1/4 d'euro. |
Mise en équation
|
|
|
Résolution (2) x 3 => |
|
|
|
(1) dans (3) => |
|
|
|
DEUX
solutions en nombres entiers |
x = 0 y = 20
z = 80 x = 15 y = 1
z = 84 |
|
|
|
||
|
Énigme J'ai acheté S animaux pour P euros dont des coqs à a euros pièce, des
poules à b euros et des poussins à c euros. |
Mise en équation
Ce système d'équations
diophantiennes et souvent nommé le problème des cent volailles (hundred
fowls problem). |
|
|
Résolution |
|
|
|
NOMBREUSES
solutions en nombres entiers pour S = P = 100 En jaune, les solutions trouvées ci-dessus. Évidemment aucune solution pour b = c (division
par 0). |
Exemples a, b, c, x, y, z S, P 5, 3, 1/3, 0, 25, 75, 100, 100 5, 3, 1/3, 4, 18, 78, 100, 100 5, 3, 1/3, 8, 11, 81, 100, 100 5, 3, 1/3, 12, 4, 84, 100, 100 5, 3, 1/4, 10, 10, 80, 100, 100 5, 3, 1/5, 5, 20, 75, 100, 100 5, 3, 1/5, 12, 8, 80, 100, 100 5, 4, 1/3, 8, 8, 84, 100, 100 5, 4, 1/4, 0, 20, 80, 100, 100 5, 4, 1/4, 15, 1, 84, 100, 100 5, 4, 1/5, 4, 16, 80, 100, 100 |
|
|
Avec
S = 100 et p = 1000, et en
conservant a = 5, il faudrait des valeurs
de b et c telles que celles-ci: |
5, 11, 1, 0, 90, 10, 100, 1000 5, 11, 1, 5, 88, 7, 100, 1000 5, 11, 1, 10, 86, 4, 100, 1000 5, 11, 1, 15, 84, 1, 100, 1000 5, 11, 1/3, 6, 88, 6, 100, 1000 5, 11, 1/7, 4, 89, 7, 100, 1000 5, 12, 1, 5, 80, 15, 100, 1000 5, 12, 1, 16, 76, 8, 100, 1000 5, 12, 1/8, 15, 77, 8, 100, 1000 5, 12, 1/15, 3, 82, 15, 100, 1000 5, 13, 1, 0, 75, 25, 100, 1000 5, 13, 1, 3, 74, 23, 100, 1000 5, 13, 1, 6, 73, 21, 100, 1000 5, 13, 1, 9, 72, 19, 100, 1000 5, 13, 1, 12, 71, 17, 100, 1000 5, 13, 1, 15, 70, 15, 100, 1000 … |
|
|
Inde: Baskali
|
Les deux solutions: a, b, c, x, y, z S, P 3, 3/2, 1/2, 0, 10, 10, 20, 20 3, 3/2, 1/2, 2, 5, 13, 20, 20 |
|
Inde: Mahavira's Ganita-sara-sangraha Les pigeons
sont vendus par 5 pour 3 panas; les grues à 7 pour 5; les cygnes à 9 pour 7
et les paons à 3 pour 9. Un homme ramène 100 oiseaux pour 100 panas. Combien
a-t-il payé pour chaque espèce ? |
Les six solutions: a, b, c, d x, y, z, t S, P 5/3, 7/5, 9/7, 1/3, 5, 25, 35, 35,
100, 100 5/3, 7/5, 9/7, 1/3, 9, 20, 35, 36,
100, 100 5/3, 7/5, 9/7, 1/3, 10, 25, 28, 37,
100, 100 5/3, 7/5, 9/7, 1/3, 13, 15, 35, 37,
100, 100 5/3, 7/5, 9/7, 1/3, 14, 20, 28, 38,
100, 100 5/3, 7/5, 9/7, 1/3, 19, 20, 21, 40,
100, 100 |
|
Europe: problème posé par Alcuin (VIe siècle) Cent
boisseaux de grains sont distribués à cent personnes: 3 pour un homme, 2 pour
une femme et un demi pour les enfants. Combien y-a-t-il d'hommes, de femmes
et d'enfants ? |
Les six solutions: 3, 2, 1/2, 2, 30, 68, 100, 100 3, 2, 1/2, 5, 25, 70, 100, 100 3, 2, 1/2, 8, 20, 72, 100, 100 3, 2, 1/2, 11, 15, 74, 100, 100 3, 2, 1/2, 14, 10, 76, 100, 100 3, 2, 1/2, 17, 5, 78, 100, 100 |
|
Arabes: Abu Kamil (850-930)
(Quelle valeur avait-il donné à
k ?) |
Exemples de solutions k = 12 3, 3/5, 1/3, 17, 80, 3, 100, 100 3, 3/5, 1/3, 18, 70, 12, 100, 100 3, 3/5, 1/3, 19, 60, 21, 100, 100 3, 3/5, 1/3, 20, 50, 30, 100, 100 3, 3/5, 1/3, 21, 40, 39, 100, 100 3, 3/5, 1/3, 22, 30, 48, 100, 100 3, 3/5, 1/3, 23, 20, 57, 100, 100 3, 3/5, 1/3, 24, 10, 66, 100, 100 |
Abu Kamil pose cette devinette
|
Énigme: Un ouvrier gagne 6 dirhams par
jour s'il travaille et doit rendre 4 dirhams par jour s'il ne travaille
pas. Ce mois d'avril, il n'a rien
gagné. Combien de jours a-t-il travaillé. Réponse: il a travaillé x jours et s'est
reposé pendant (30 – x) jours. Soit la relation: 6x = 4(30 – x) ou 10x = 120
et x = 12 jours de travail et 18 jours de repos. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()