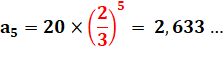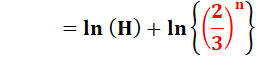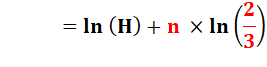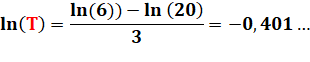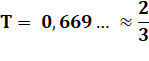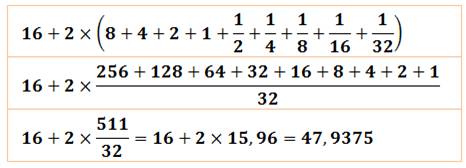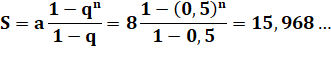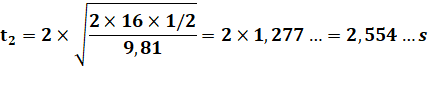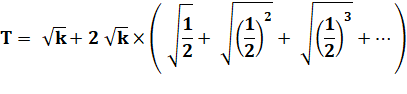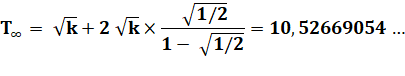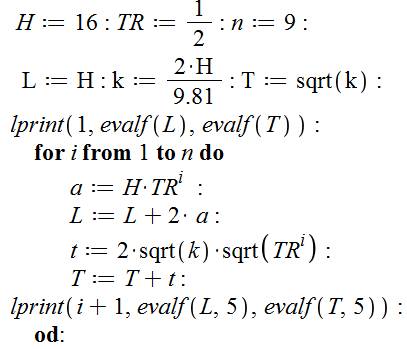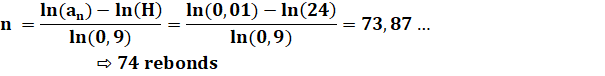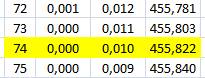|
||||||||||||||||||||||||||||
![]()
|
Lâchée d'une certaine
hauteur la balle rebondit selon un certain taux
de rebond. Comment calculer la hauteur (altitude)
atteinte au énième rebond? Quand
atteint-elle une altitude spécifiée? Etc. Tour de la question en
commençant par des calculs abordables dès le collège et en introduisant des outils accélérant les calculs. Une manière d'enrichir nos
connaissances. |
Anglais:
bouncing ball
|
Je voudrais commencer tout en douceur sans regarder ce
tableau >>> Ce que nous allons calculer (flèche
rouge) en connaissant les paramètres en jaune.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec quels outils mathématiques? Simples opérations >>> Puissances >>> Fractions au même
dénominateur >>> Logarithmes et exponentielles >>> Progression géométrique >>>
|
Avec quels outils informatiques ? Calculette >>> Tableur >>> Programmation >>> |
|||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|||
|
Énigme La balle
en caoutchouc est lâchée d'une hauteur de 50 mètres. Elle
rebondit à chaque fois au deux tiers de sa hauteur. Calculez
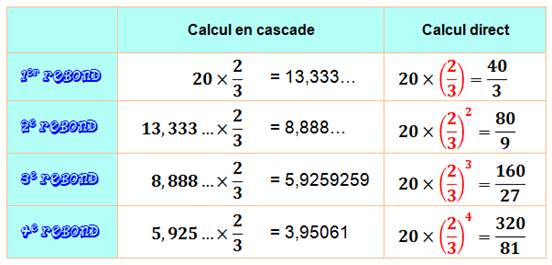
l'altitude pour les quatre premiers rebonds. Calcul Un petit
dessin et un calcul avec calculette est suffisant. En effet,
pour passer d'un rebond au suivant, on prend les 2/3 de la valeur de
l'altitude précédente. Simples opérations courantes |
|
||
|
La
colonne centrale montre le calcul fait au fur et à mesure. La
colonne de droite montre comment la formule de calcul se transforme à chaque
rebond suivant. |
|
||
|
|
||
|
Nous
déduisons la formule générale avec 2/3
à la puissance n. |
|
|
|
Facile de
calculer l'altitude "a5"
du cinquième rebond |
|
|
|
|
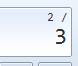
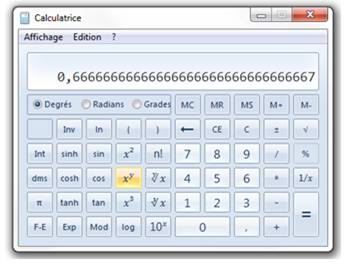
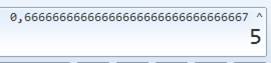
Détail du calcul Avec la calculette de votre ordinateur 1)
Commencez par entrer la division de 2 par 3 avec le clavier numérique ou en
désignant les touches de la calculette avec la souris. 2) Pour
élever à la puissance 5, appuyez sur la touche xy (ici, illuminée
en jaune). 3) Puis
sur la puissance désirée, ici 5. 4)
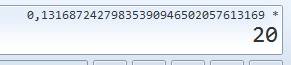
"Entrez" donne le résultat: 0,131 … 5) Multipliez
par 20. 6)
"Entrez" donne le résultat final. |
|
|
Essayez
pour le dixième rebond: |
|
|
|
Le
centième …. proche de zéro. |
|
|
|
|
||
|
Pour quel
rebond l'altitude sera inférieure à 1 mètre pour la première fois. |
Connaissant a, calculer n |
|
|
Évidemment
on peut toujours faire le tableau et constater le dépassement. En
l'occurrence, le septième rebond est toujours au-dessus du mètre, mais le
huitième est en dessous. Nous
allons utiliser la calculette pour obtenir ce résultat avec un seul calcul.
Pour cela, nous allons transformer la formule en prenant le logarithme de
chaque côté. |
|
|
|
Le logarithme est magique, il
transforme
Alors, la
formule devient => |
|
|
|
Formule
pour le calcul de n. |
|
|
|
Application
numérique à notre cas. Il faut dépasser
le septième rebond pour atteindre une altitude de 1 mètre. Au huitième rebond
la balle est en-dessous du mètre. |
|
|
|
|
Détail du calcul 1) Pour calculer ln(1),
entrez 1 puis appuyez sur la touche ln. Résultat 0. En effet ln(1) = 0. 2) Soustraire ln(20) =
2,995… 3) Appuyez sur la touche
diviser, entrez la parenthèse, tapez 2 puis ln, appuyez sur -, puis entrez 3
et ln, fermez la parenthèse. 4) Faites entrez. Résultat
7,388… |
|
|
|
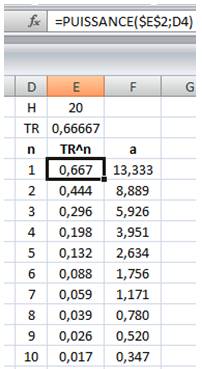
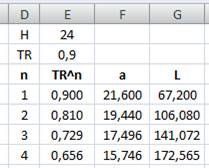
Les
paramètres H (hauteur du lâcher initial) et TR (taux de rebond) sont
spécifiés. La
quantité de rebonds (n) est déclinée de 1 à 10. La
puissance du taux (2/3)n est calculée sur la colonne E. La formule
est indiquée dans la fenêtre en haut. Notez que le "$" indique
qu'il faut toujours prendre la valeur de H en E2. La
colonne F est la simple multiplication de la colonne E par 20. Note: l'utilisation du tableur peut s'avérer très utile
pour vérifier un calcul formel. |
|
|
||
|
La balle
est lâchée de 20 mètres et atteint une altitude de 6 mètres au troisième
rebond. Quel le
taux de rebond? |
Connaissant H, n et an, calculez T |
|
|
Passage
aux logarithmes. |
|
|
|
Pour
calculer T. |
|
|
|
Dans
notre cas. |
|
|
|
Inverse
du logarithme (exponentielle). Nous
retrouvons bien le taux initial de notre problème. Note: le taux est
légèrement différent car nous avons pris 6 m au lieu de 5,925… mètres |
|
|
|
|
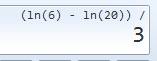
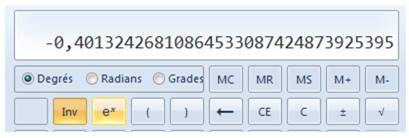
Détail du calcul 1) Ouvrez la parenthèse,
faites ln(6) – ln(20) et fermez la parenthèse pour diviser le tout par 3.
Résultat -0,401… 2) Appuyer sur la touche
inverse, la touche logarithme devient exponentielle (la fonction inverse du
logarithme). 3) Appuyez sur la touche ex
et le résultat cherché est 0,669… |
|
|
La formule du
rebond parfait est: Nous sommes
capables avec une calculette et sa touche logarithme de calculer n'importe
quel paramètre en connaissant les autres. évidemment dans la
réalité, la balle ne rebondira pas éternellement. Le cas de la balle idéale
fait penser au paradoxe
de Zénon. |
|
A
reboncing ball rebounces each time to a height equal to one half the height
of the previous bounce. If it is dropped from a height of 16 meters. Find the
total distance it has travelled when it hits ground for the 10th time. |
|
|
||
|
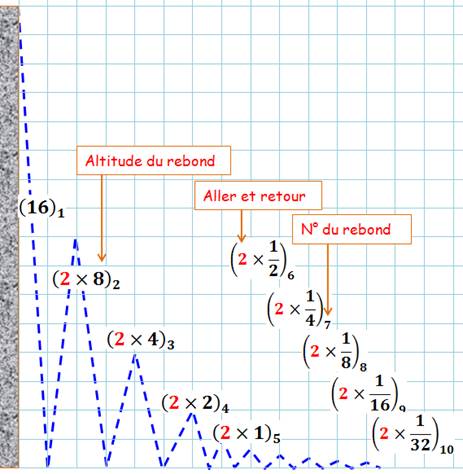
Le cas en
anglais (ci-dessus) demande à calculer le trajet total de la balle partant de
16 mètres et arrivant à son 10e rebond. La balle rebondit à chaque
fois de sa demi-hauteur. La figure
montre que la balle tombe une fois de sa hauteur et "s'envole" neuf
fois pour atteindre le dixième rebond. Il s'agit
donc de calculer la somme 16 + 2(8
+ 4 + 2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32). On peut la calculer à la main ou avec une calculette.
Je propose deux méthodes plus mathématiques ci-dessous avec mise
au même dénominateur. En
remarquant que la somme
des puissances de 2 est connue. Au
dixième rebond, la balle a parcouru presque trois fois la hauteur de chute:
48 mètres. Alternative ce calcul Calcul
d'une progression
géométrique de raison q = ½ et
point de départ 8: |
NB. Le déploiement horizontal est une facilité
d'explication
|
|
|
|
|||
|
La balle
en chute
libre |
|
||
|
Temps de
chute avec g = 9,81 m/s² |
|
||
|
Premier
rebond, aller et retour |
|
||
|
Le
tableau montre les calculs réalisés. La balle a
mis 10,14 secondes pour atteindre le dixième rebond. La
formule s'écrit génériquement de la manière suivante, en posant k = 2 x 16 / 9,81:
Avec
calcul de la limite de la série géométrique
Une balle lâchée à 16 mètres
de hauteur et rebondissant de moitié à chaque rebond met 10 secondes et demi
pour s'amortir complètement. Lâchée de 100 mètres, elle mettrait 26,31
secondes. |
|
||
|
|
Initialisation
des paramètres: H, hauteur du lâcher; TR, taux de rebond; n, nombre de
rebonds en plus du premier. Initialisation
de L, la longueur parcourue par la balle; k, le coefficient dans la formule
du temps et T, le temps de trajet. Impression de cette première valeur pour
le rebond n°1. Lancement
d'une boucle de 1 à 9 pour les rebonds de 2 à 10. Calcul
de a, l'altitude de chaque rebond et cumul en L. Calcul de t, la durée d'un
demi-rebond et cumule en T. Impression
du numéro de rebond, la longueur parcourue et, en quel temps. Fin de
la boucle (od:) En
bleu, l'impression demandée. |
|
Problème Lucas lâche une
balle d'une hauteur de 24 m. On estime que, lorsque la balle rebondit, la
hauteur de son rebond perd 10% par rapport au précédent rebond. On considère
que la balle ne rebondit plus lorsque la hauteur du rebond et inférieure à 1
cm. 1. Combien de
rebonds (n) effectue la balle de Lucas ? 2. Quelle distance
(L) parcourt-elle avant de ne plus rebondir ? Résolution question 1.
Résolution question 2.
Vérification par tableur (Voir Explications)
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()