|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|
|
|
|
|
|
|
|
=>
soit 10 x 6 = 60 couples qui dansent
=>
soit F x 4 = 60 couples qui dansent
=>
il y en a: F = 60 / 4 = 15. |
|
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Chacun des perdants a bien joué un match. C'est la réponse: 1024 matches. Ce serait vrai avec n'importe quel nombre! Autre méthode
|
|
![]()
|
|
||
|
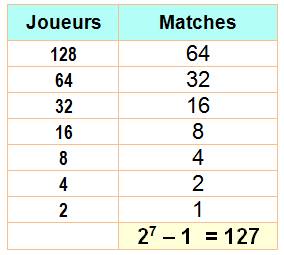
Pour un tournoi 128 joueurs
sont inscrits en simple dames. Combien de parties pour
arriver en finale? Les 128 joueurs disputent 64 matches qui laissent 64 joueurs en
compétition. Ces 64 joueurs disputent 32 matches qui laissent 32 joueurs en
compétition. Etc. |
|
|
|
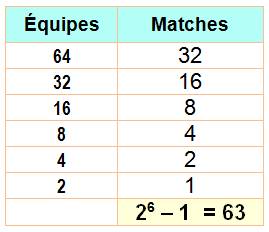
Pour un tournoi 128 joueurs
sont inscrits en double dames. Combien de parties pour arriver
en finale? Oubliez qu'ils sont deux et comptez en équipes: 128 joueurs forment 64
équipes de doubles. Les 64 équipes disputent 32 matches qui laissent 32 équipes en
compétition. Etc. |
|
|
|
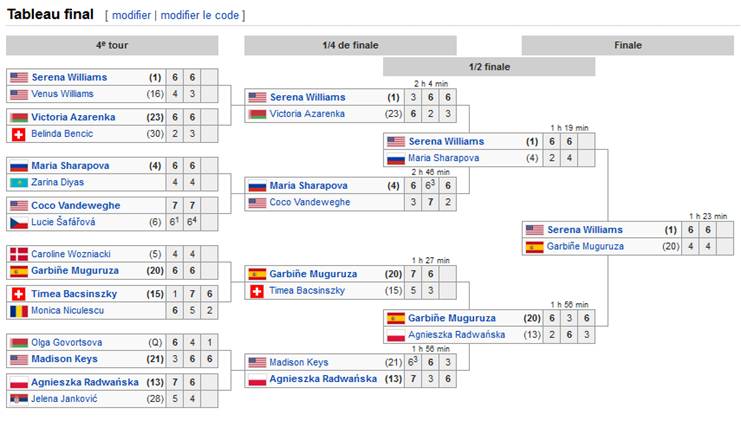
Exemple de tableau (simple dames Wimbledon 2015
16 joueuses 8
joueuses 4
joueuses 2
joueuses Source: Tournoi de
Wimbledon 2015 - Wikipédia |
||
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Cette page |
![]()